1 Exploring patterns and processes

Suppose you are tiling a bathroom or kitchen and the last row of square tiles is to be a frieze made up of blank tiles and patterned tiles as shown below.

Figure 1

A friend has offered to help. How would you describe the pattern and how to arrange the tiles?

There are lots of ways of tackling this. For example, you might say that you will need some blank tiles and some patterned tiles with the ‘bridges’ on. Start with a bridge tile, then put a blank tile next to it. Take another bridge tile, but turn it round so that the bridge is upside down, like a smile and put it next to the blank tile in the same line. Then put another blank tile next to the smile tile. This is the pattern, just carry on: bridge, blank, smile, blank, bridge, blank, smile, ….

Or you may have decided to draw a picture of the tiles, or demonstrate the pattern with the tiles themselves. Whatever you do though, it's probably easier to remember and apply if you have recognised that the pattern is a four-tile repeat with the two different types of tile.

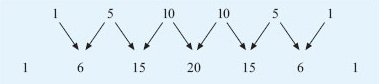
The frieze is an example of a type of geometrical pattern that has many applications in art, crafts and design. The next example is a number pattern which appeared in China and Persia over 700 years ago, but is still used by students in mathematical and statistical problems today and it even appears in chemistry. It is known as Pascal's triangle (named after Blaise Pascal who was a 17th century French mathematician who studied the properties of this triangle) and the first part of it is shown below.

Figure 2

You can continue the triangle indefinitely by following the pattern.

Each row of numbers starts and ends with the number 1. Look at each pair of numbers in the last line above. For each pair, add the two numbers together and write their sum on the line below as shown. This process generates the next row of the triangle.

Figure 3

Activity 1: Pascal's triangle

Using the hexagonal paper attached in PDF format below, write down the numbers in the next two rows of Pascal's triangle.

Hexagon paper [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)]

• Can you spot any patterns in the numbers in the triangle?

• What do you notice about the sum of the numbers in each row?

• If this pattern continues, what do you think the total for the 10th row will be?

Keep this paper handy as you will need your triangle later in the course.

Discussion

The next two rows are 1, 7, 21, 35, 35, 21, 7, 1 and 1, 8, 28, 56, 70, 56, 28, 8, 1.

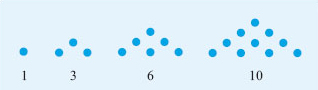
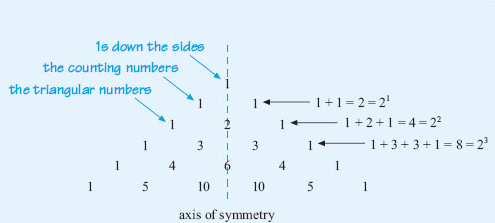
There are many different patterns. The 1s down the sides of the triangle is probably the easiest one to spot! You can also see the counting numbers 1, 2, 3, 4, 5 in the diagonal rows next to the sides. In the next diagonal row, there is the sequence 1, 3, 6, 10, …. These numbers are known as the triangular numbers because they create triangular patterns.

Figure 4

The triangle is symmetrical too. If you draw a vertical line down through 1, 2, 6, …, one side of the triangle is a mirror image of the other.

Figure 5

Do not worry if you did not spot all these patterns!

Looking at the diagonal row of triangular numbers, if you add any two adjacent numbers together, you get the square numbers. For example, 1 + 3 = 4 which is the same as 2²; 3 + 6 = 9 which is the same as 3², and so on.

The pattern in the powers suggests that the first total, 1, might be written as 20. Check on your calculator to see if this is correct. Does any number to the power 0 give you 1?

Now, if you add together the numbers in each horizontal row, you get the following pattern: 1, 2, 4, 8, 16, 32, 64, …. The total for the next row is double the total for the current row. Assuming this pattern continues, the total for row 8 will be 128, row 9 will be 256 and row 10 will be 512. You might have spotted that these numbers can also be written as 1, 2¹, 2², 2³, 2⁴, ….

What have these two examples to do with mathematics? Well, recognising patterns in shapes, sets of numbers, processes or problems generally and spotting what is the same and what is different about situations often makes the task easier to solve. You saw how recognising the tiling pattern makes it easier to remember and by using the number patterns in Pascal's triangle, you could work out the sum of each row without adding up the individual numbers. If you can spot a pattern and then describe what happens in general, this can lead to a rule or formula. Provided you can prove that this rule will always work, it can then be used elsewhere. For example, if you can work out the general process for calculating a quarterly electricity bill and then give these instructions to a computer, many electricity bills can be generated, printed and sent out in just a few minutes!