2 Looking for relationships

In this section, we are going to consider the relationship between quantities in two practical situations and see how to describe these relationships by writing down a general rule or a word formula.

Suppose you are planning a visit abroad. Your map marks all the distances between places in kilometres rather than miles. How can you work out what these distances are in miles?

Figure 6

The first bit of information you will need is how long one kilometre is, if it is measured in miles.

According to a dictionary, 1 km is equivalent to approximately 0.6214 miles.

The next step is to work out the mathematical process you will need to use to change kilometres into miles. You may be able to see how to convert from kilometres into miles immediately, but, if not, try to visualise a few simple examples first. Drawing a diagram often helps!

Each km is the same as 0.6214 miles as shown below.

Figure 7

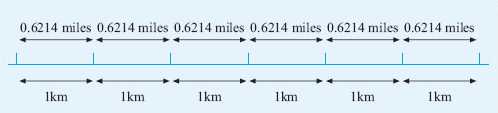
So if the distance is 3 km, you will have 3 lots of 0.6214 miles; if the distance is 10 km, you will have 10 lots of 0.6214 miles; if the distance is 250 km, you will have 250 lots of 0.6214 miles, and so on.

You can write this down mathematically as:

  250 km = 250 × 0.6214 miles = 155 miles (to the nearest whole number).

Notice that in each of the examples above, the process for calculating the number of miles was the same: multiply the number of kilometres by the conversion rate of 0.6214. This technique will work for any distance and can be written down concisely as the following word formula:

  distance in kilometres × 0.6214 = distance in miles.

This is the same as writing:

  distance in miles = distance in kilometres × 0.6214.

You can use this formula to convert any distance in kilometres into miles. For example, suppose you wanted to convert 500 km. Using the formula and replacing ‘distance in kilometres’ by 500 gives

  distance in miles = 500 × 0.6214 = 310.7.

So 500 km is equivalent to approximately 311 miles.

In this example, you used the formula by replacing the phrase ‘distance in kilometres’ in the right-hand side of the equation by the corresponding value, 500. This is known mathematically as substituting the value into the formula.

Activity 3: Exchanging currencies

Suppose you wish to exchange some money in pounds sterling into euros. At the time of writing, one agency had an exchange rate of €1.48 to £1 and did not make any additional charges. (If you prefer, you can look up the current conversion rate in a newspaper or at a bank or travel agency.)

• a.How many euros would you get for £5?

  How many euros would you get for £10?

• b.Write down a word formula that you can use to convert pounds into euros. Your formula should start ‘number of euros = …’.

• c.Check that your formula works by using it to convert £5 into euros.

Discussion

(a) For each pound, you would get €1.48, as shown below.

Figure 8

So, if you exchange £5, you would get five lots of €1.48.

So £5 = 5 × €1.48 = €7.40.

If you exchange £10, you would get 10 lots of €1.48.

So £10 = 10 × €1.48 = €14.80.

(b) To change pounds into euros, you need to multiply the number of pounds by the exchange rate of €1.48. So the word formula is

  number of euros = number of pounds × 1.48.

(c) Substituting 5 for ‘number of pounds’ gives

  number of euros = 5 × 1.48 = 7.40.

This agrees with the answer in part (a).

What would happen to the formula if there was also a handling charge?

These two examples illustrate how a word formula can be used to summarise some mathematical process such as converting units of length or currencies. Once a formula has been derived, it can then be used in other situations, both for calculations by hand or by computer, for example for currency transactions in a bank. You will be able to practise writing down some more of your own formulas in Sections 4 and 5.