9 Patterns in nature and elsewhere
If you take a cauliflower and break off one of the florets, the floret appears to be just the same shape as the original cauliflower but on a much smaller scale.

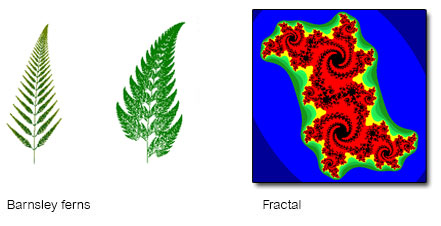
This idea of self-similarity occurs throughout nature – the frond of a fern looks like the whole fern, a branch of a tree splits into further branches which look like trees themselves, and so on.
Self-similarity now forms part of an area of mathematical research known as fractal geometry. Beautiful patterns can be generated by fractal formulas, such as the Barnsley fern and the fractal below. Fractal geometry also has many practical applications in the physical sciences, medical research, economics and computing, particularly in compressing images.
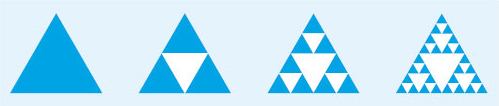
You can generate part of a fractal yourself, by using Pascal's triangle that you constructed earlier in the course. If you shade in (or cover) all the odd numbers in the triangle, a pattern starts to emerge as shown below.

This is part of a fractal known as Sierpinski's triangle (Waclaw Sierpinski (1882–1969) was a Polish mathematician). It can also be generated by starting with a triangle, splitting it into four smaller triangles and removing the middle one. Then split each of the remaining triangles into four smaller triangles and remove the middle one. Carrying on in this way results in something like the sequence below.