5.2 Material comparisons
I want to depart from the specific example of the bicycle to make some more general points.
In most simple structural analysis the self-weight of the structure is ignored, as it is considered to be small in comparison with the loads carried. However, as an illustration of engineering practice in the search for efficient structures to employ in product design, it is worth examining how the strength and weight of particular materials compare.
These comparisons are illustrated through the use of modelling. As an example, let's estimate the maximum length of a hanging tie-rod and the maximum height of a column. See Box 9 Long ties and high columns.
Box 9 Long ties and high columns
Figure 26 shows a parallel-sided rod of material of density ρ and yield stress σy hanging from a support.
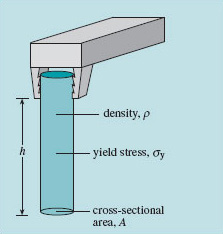
The stress in the cross-sectional area A increases on each horizontal plane as you go up the rod. It will fail by yielding in the uppermost section when the stress there reaches the yield stress, which is a characteristic of the material. If this occurs when the rod is h metres long, we can say that:
Force on the failure plane
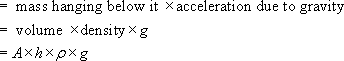
If the material yields then the force on the plane at failure =
A × σy.
Hence, equating these values gives:
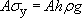
Therefore,
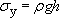
Notice that the cross-section term A cancels out from the equations.
Example
A mild steel has a density of 7800 kg m−3 and yield stress 300 MN m−2 What is the maximum length of rod that could be dangled from a high building without yielding under its own weight? Take g = 9.8 m s−2.
Answer
Using the equation σy = ρgh, and rearranging:
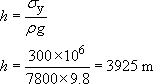
Hence the rod could be almost 4 km long before it would break under its own weight.
But could we build the tower from which to hang this extremely long rod?
Example
Consider building a brick tower from which we could suspend a rod for testing. Brick has a crushing strength σc of 70 MN m−2 and a density of 2000 kg m−3. What is the maximum height of a parallel-sided tower that can be built without crushing the bottom course of bricks? Assume the mortar thickness to be negligible and of higher strength.
Answer
The relevant equation comes from relating the weight of bricks above the bottom layer to the force required to crush it. The result is:
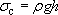
The crushing strength and density of the brick are inserted into the formula to give:
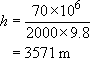
That's right, over 3.5 km (2 miles) high!
Hence the crushing strength of brick would limit the construction of a tower to test the steel rod. You would have to taper it to be narrower at the top.The limiting equation for both long ties and struts is:
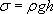
Rearranging this gives a general expression for maximum length in terms of the maximum self-supporting height:
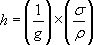
Now (1/g) is a constant, and if g stays constant h is proportional to (σ/ρ). This quantity is a measure of a material's ability to support itself in tension or compression (depending on which value is used for the strength). It is called a 'merit index for self-supporting strength. This means long self-supporting ties and long self-supporting struts are more feasible if the merit index (σ/ρ) is big. Not surprisingly, this occurs with high-strength, low-density materials.
