10 The decibel
10.1 Introduction
For a variety of reasons, not least the very wide dynamic range of human hearing, the decibel (symbol dB) is often used as a unit for the amplitude of sound waves. The decibel is also used in other contexts, such as specifying the amplification of amplifiers or the degree to which a signal is affected by noise. In the context of sound, the use of the decibel as a unit captures something of the subjective impression of the way loudness changes with amplitude.
The decibel unit has two rather unusual properties in comparison with other more conventional units you have probably met, such as the metre or the second:
It indicates a ratio, rather than an absolute value. Thus the decibel can be used as a way of comparing one amplitude with another.
Equal decibel increments correspond to equal multiplications of ratio.
Because the decibel expresses a ratio rather than an absolute value, it cannot by itself specify the absolute amplitude of a sound. I shall explain shortly how it can be adapted for the expression of absolute values, but first I want to pursue the second feature I listed above, namely that equal decibel increments correspond to equal multiplications of ratio. I want to do this in the context of ratios of amplitude.
Figure 27 relates ratios to their decibel equivalents, and Table 1 does the same thing for a few discrete values.
| Decibels | Amplitude ratio |
|---|---|
| −12 | 0.25:1 |
| −6 | 0.5:1 |
| 0 | 1:1 |
| 6 | 2:1 |
| 12 | 4:1 |
| 18 | 8:1 |
| 20 | 10:1 |
| 24 | 16:1 |
| 30 | 32:1 |
| 36 | 64:1 |
| 40 | 100:1 |
| 60 | 1000:1 |
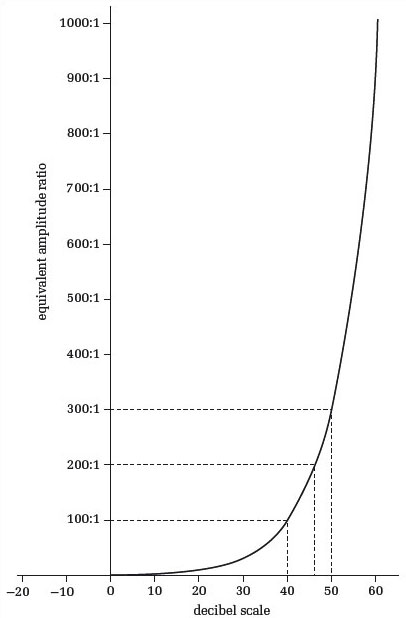
One thing that is immediately clear from Figure 27 is the exponential relationship between decibels and their equivalent amplitude ratios. For instance, the graph shows that an amplitude ratio of 100:1 has a decibel equivalent of 40 decibels, but an amplitude ratio that is twice as big (200:1) does not have 80 decibels as its decibel equivalent. In fact its decibel equivalent is about 46 decibels. A proportional relationship between decibels and their corresponding amplitude ratios would have a straight-line graph. Notice also (from Table 1) that 0 dB corresponds to a ratio of 1:1, and that for ratios between 1:1 and 0:1 the decibel equivalent has a negative value.
In the first part of the audio track for Activity 30 you heard a sound clip that doubled in amplitude at each reappearance. However, the sound appeared to be getting louder by an equal amount each time. What does a doubling of amplitude look like when measured in decibels? Let's say that the starting amplitude of the sound was 1 unit on a convenient scale of pressure or voltage. In Table 2 the first column shows the successive amplitudes of the waves that you heard in terms of this unit. Notice that in each line of the table the amplitude is twice that in the line above.
| Amplitude | Amplitude ratio | Decibel equivalents |
|---|---|---|
| 1 unit | 1:1 | 0 dB |
| 2 units | 2:1 | 6 dB |
| 4 units | 4:1 | 12 dB |
| 8 units | 8:1 | 18 dB |
| 16 units | 16:1 | 24 dB |
The second column gives these amplitudes as a ratio of the starting amplitude in the first line. The third column expresses these ratios in decibels, using data from Table 1.
Activity 31 (Exploratory)
How do the values in the decibel column of Table 2 increase from line to line?
Discussion
The decibel value on each line is an equal increment on the decibel value in the line above. The increment is 6 decibels each time. Thus in the first part of the audio track in Activity 30 there was a 6 decibel increase of amplitude with each recurrence of the sound.
The equality of the decibel increment you saw in the last activity therefore matches our subjective sense of equal increments of loudness when the amplitude is multiplied by a constant factor (2 in this case).