1.2.1 Heating and cooling the Earth: the overall radiation balance
The Sun emits electromagnetic radiation with a range of wavelengths, but its peak emission is in the visible band - the sunlight that allows us to see. The wavelength of radiation has important climatic implications, as we shall see shortly. For now, we are mainly interested in the overall rate at which energy in the form of solar radiation reaches the Earth.
SAQ 1
What is the SI unit for the rate of energy transfer, or 'power'?
Answer
The watt (W), defined as 1 W=1 J s−1 (joule per second).
Radiation streams out of the Sun at the prodigious rate of 3.85 × 1026 W. Located at an average distance from the Sun of some 150 × 106 km, the Earth intercepts only a tiny fraction of this - an amount equivalent to the solar radiation falling on the flat, circular disc depicted in Figure 2. Note that we imagine the disc to be just outside the Earth's atmosphere and aligned at right angles to the Sun's rays: the solar input per unit area (a square metre, say) of this disc is called the solar constant. Measurements from satellite-borne radiation sensors give the solar constant an average value over recent years of 1368 W m−2. Of course, the Earth is a rotating sphere, not a flat disc. As explained in the paragraph below Figure 2, when averaged over the surface of the whole globe, the solar input per unit area at the top of the atmosphere comes down by a factor of four, to 342 W m−2. For simplicity, we shall refer to this globally averaged value as '100 units', though you should remember that these are units of 'energy per unit time per unit area'.
Not all of the incoming solar radiation is available to heat the Earth: some of it is reflected directly back to space. The proportion of incident solar radiation that is reflected by a given surface is called the albedo. Now have a look at Figure 3. This is an image of the Earth from space formed from reflected sunlight (solar radiation at visible wavelengths). Clouds and the ice-covered mass of Antarctica (at the bottom of the image) appear bright because they reflect strongly; i.e. they have a high albedo - up to 90% in the case of fresh snow and sea-ice. By contrast, the oceans have a low albedo (typically less than 5%) and appear dark in this image. In general, most land surfaces have moderate albedo, with values ranging from 10-20% for forests to around 35% for grasslands and deserts.
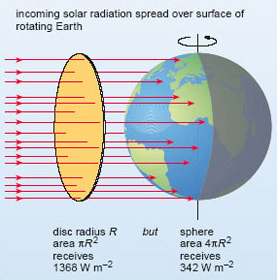
Figure 2 The Earth intercepts an amount of solar radiation equivalent to that falling on a disc with the same radius (R ) as the Earth, facing the Sun: this comes to (1368 × πR2 ) W, where πR2 is the area of the disc (in m2). However, the Earth is spherical , so the area presented to the incoming solar radiation by the rotating Earth (over a period of 24 hours or more) is 4πR 2; i.e. four times as great. Thus, the solar input per unit area averaged over the surface area of the whole Earth is a quarter of the solar constant; i.e. 1368 Wm−2/4=342 Wm−2.

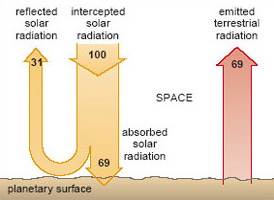
Evidently, the albedo can vary markedly around the world, depending on the cloud cover and surface characteristics. The planetary albedo is the combined figure for the Earth as a whole: on average, it has a measured value of 31% (31 units). The remainder (69 units) is absorbed by the atmosphere and materials at the Earth's surface (the oceans, soils, vegetation and so on).
SAQ 2
What is the rate per unit area at which solar energy is absorbed by the Earth's atmosphere and surface?
Answer
69 units is 69% of 342 W m−2 or (342 W m−2) × (69/100)=236 W m−2.
Suppose now that the Earth's atmosphere is stripped away, but the planetary albedo is unchanged. (This may strike you as a curious proposition, but it will help to expose just how important the atmosphere really is.) The energy flows at the surface of this 'airless' world are shown in Figure 4. To the left of the figure, a nominal 100 units of solar radiation reach the planet; 31 units are reflected away and all of the remaining 69 units are absorbed by the surface.
SAQ 3
By itself, what would be the effect of this continual input of solar energy?
Answer
The surface would warm up; indeed, it would get progressively hotter and hotter.
Fortunately, there is a compensating cooling effect. Like the Sun, all objects (you and I included) emit electromagnetic radiation. Further, they do so at a rate that depends on the temperature of the object: the hotter an object becomes, the higher its radiative power - the rate at which it emits radiation. For our planet, a steady or equilibrium temperature is maintained by a dynamic balance: the rate at which solar energy is absorbed (the 69 units to the left in Figure 4) must be balanced by the rate at which the planet loses energy to space as emitted radiation (the 69 units to the right in Figure 4). Note that this emitted radiation originates with the 'jostling about' of atoms within the surface; it is not the same thing as the reflected solar radiation, which merely 'bounces off' the surface. To emphasise the distinction, we shall refer to the radiation emitted by the planet as terrestrial radiation.
Expressed in quantitative terms, the relationship between temperature and radiative power is the basis for a well-established law of physics. The appropriate calculations tell us that, for an Earth-like planet to emit radiation to space at a steady rate of 236 W m−2 (the 69 units depicted in Figure 4), it should have an equilibrium temperature of -19 °C.
This equilibrium temperature is known as the effective radiating temperature and, were it not for the atmosphere, this would also be the Earth's global mean surface temperature. Conditions would certainly be inimical to life as we know it. But how does the atmosphere perform the vital trick of keeping the GMST at a more temperate 15 °C (? The answer is bound up with an important difference between 'solar' and 'terrestrial' radiation - one that again depends on the temperature of the source.
Question 1
Heated in an ordinary fire, a metal poker glows 'red-hot'; if heated to a higher temperature (in an oxy-acetylene flame, say), it would glow 'white-hot'. Generalising from this example, does the average wavelength of emitted radiation increase or decrease as the temperature of the emitting body rises? Include your reasoning.
Answer
White light contains all visible wavelengths (Box 1), whereas red light is at the long wavelength end of the visible band (Figure 1). 'White-hot' objects therefore emit light of shorter average wavelength than cooler 'red-hot' ones. Generalising, as the temperature of an object rises, so the average wavelength of the radiation it emits will decrease.
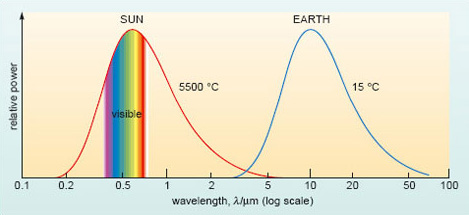
The trend you identified in Question 1 is evident in Figure 5. Here, the curves record the distribution, or spectrum, of wavelengths emitted by the Sun (with an average surface temperature of some 5500 °C) and the Earth (with a GMST of 15 °C). The plots are schematic, in the sense that the vertical scale is not defined, but each shows how the radiative power is apportioned among the range of wavelengths emitted.
SAQ 4
With reference to Figure 5, is it reasonable to use 'shortwave' and 'longwave' as a shorthand for incoming solar radiation and outgoing terrestrial radiation, respectively?
Answer
Yes. The two curves in Figure 5 barely overlap: solar radiation peaks in the visible band, although there are contributions at both shorter wavelengths (in the ultraviolet, uv) and longer wavelengths (in a region often called the 'near' infrared). By contrast, radiation emitted at cooler terrestrial temperatures lies entirely at longer infrared (ir) wavelengths.
This pattern is important because the atmosphere is relatively transparent to incoming shortwave radiation, but not to outgoing longwave radiation. And that has a profound effect on the actual energy balance at the Earth's surface.
