4.3 Thermally activated processes
Thermally activated processes are those that get going not because of average effects, but because the fraction of particles in the tail of the distribution increases with temperature. This is a basic property of the thermal distribution we have been discussing. For instance, what would take 30 000 years at room temperature may happen in under one second at 1000 K if it depends on how many particles have an energy in excess of 1 eV.
The next step in the study of energy distributions and temperature is therefore to see how the distributions in Figures 13(b) and 14 can be described by a mathematical expression from which meaningful numbers can be obtained.
The thermal energy distribution I have been using in Figures 13(b) and 14 is described mathematically by the following relationship:
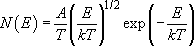
where A is a constant, and N(E) and E are as in Figure 14. In this expression, since T is in units of kelvins, E/k must also be in kelvins.
That means that an energy in joules must be combined with Boltzmann's constant (k = 1.38 × 10−23 J K−1). If the energy is in electron volts, k must be replaced by k/e which is 86 × 10−6 eV K−1.
What we need from the mathematical form of the distribution is a way of quantifying how the proportion of energetic particles changes with temperature.
Given the above mathematical form it is possible to show that the fraction of particles having energy greater than say E 1 is approximately proportional to (E1/kT)1/2exp(−E 1/kT), provided E1 is much greater than kT. Under these circumstances the exponential part changes much more rapidly than the square root and therefore the fraction of particles having energies exceeding E1 predominantly varies exponentially, according to the function exp(−E1/kT).
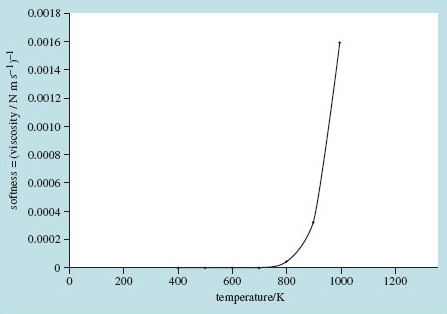
Rates of chemical reaction, some of the electrical properties of materials, the diffusivity of impurities in silicon and the 'softness' of glasses – all show this kind of dependence on the exponential of a characteristic energy compared with absolute temperature (Figure 15).