2.2d – Calculating energy in the elastic store
The equation for the energy stored in spring is:
The SI units for energy are joules (abbreviation J), which are used if the extension is measured in metres and the spring constant is measured in newtons per meter.
Example elastic store question
What is the energy stored in this spring when it has been stretched by 10 cm?
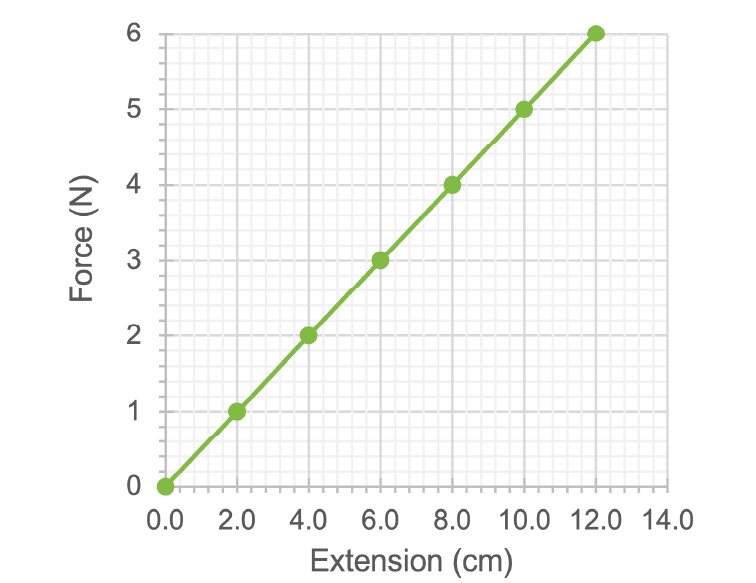
First, let’s write what we definitely know:
Now, let’s determine the spring constant:
Finally, we can put it into the energy equation:
Note - if students understand that the energy stored is the area under a graph, then they can go straight to the answer without doing the intermediate calculation.
The most likely mistake on these questions is in forgetting to convert the extension into meters.
Deriving the elastic store equation
If students are supported to analyse the graph carefully, they can discover for themselves where these odd terms come from, and it’s gratifyingly straightforward. As well as satisfying a natural curiosity by explaining this properly, it can also help students to understand what is happening as a spring is stretched.
Read through the following. They are the sort of questions that you can ask students as you teach graph springs. For each question jot down your answer in your blog before you move onto the next step.
Whilst many, and probably most, students are happy if they can just recall and use the equations that describe the different stores, at some point most students facing the equation of a stretched spring will ask the difficult question, “where does
the half and the squared come from?”
Q1) Describe in words what you would feel as you stretch this spring to
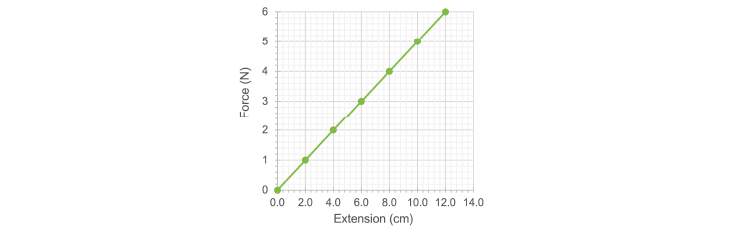
A1) At first it is easy to stretch, but as it gets longer it also puts up more resistance – it is pulling back harder.
As we have seen, you can determine the energy used in pulling something along by calculating . In the case of a stretched spring, you cannot do this because the force is also changing.
With a spring you need to work out the area under the graph; this takes into account the fact the force is changing as you increase the extension. Working out the area under the graph is the same as trying to add up lots of super-narrow rectangles that are constantly increasing.
Q2) How much larger than the area under the graph between and will the area under the graph be between and ? Note, you do not actually need to calculate it, you can just compare the size of the triangles.
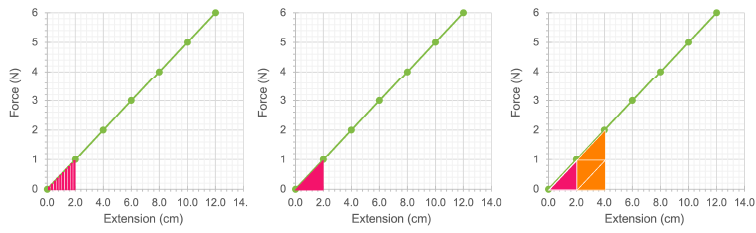
A2) We can see from the graph that the area of the orange and pink triangles is four times the size of the pink triangle by itself. Therefore, it takes four times the amount of energy to stretch a spring by twice the distance.
Q3) How much larger than the area under the to graph is the area between and ? Try to visualise the extra triangles required.
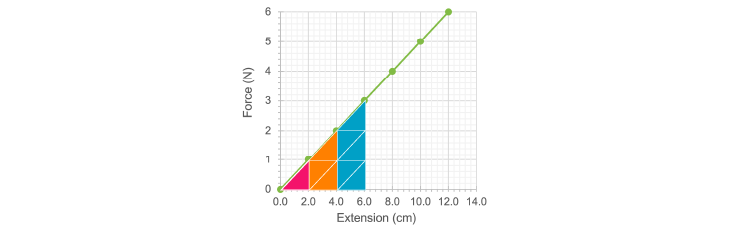
A3) It takes 9 times the energy to stretch a spring by three times the distance.
From this, we can see that as you increase the extension of a spring, the energy stored by that spring (and therefore the energy needed to stretch that spring) will increase with the square of the extension.
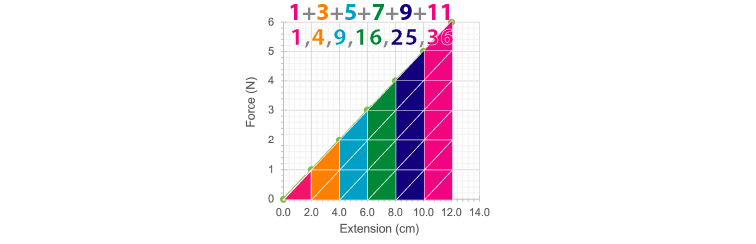
This should show, without the need for difficult calculations, that work done is proportional to the square of the extension.
We can determine the actual work done by calculating the area under a force-distance graph. To work out the area of a triangle we do half base times height. For the graph of the spring the base of the triangle is the extension, , and the height of the triangle is the force, which can be calculated by doing .
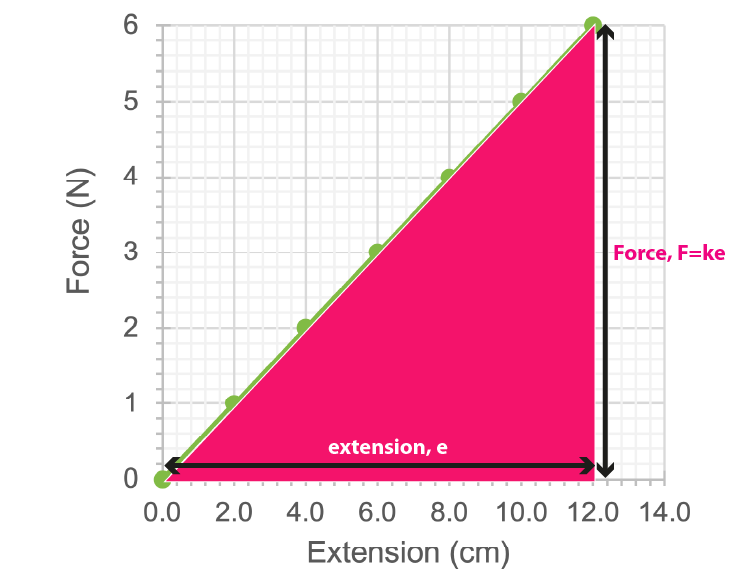
We can calculate the energy stored in a spring by calculating the work done in stretching the spring.
This gives us the final equation:
2.2c – Calculating energy in the kinetic store
