1.2 The toxicity of chemicals
As you have just considered several safe levels for chemicals in drinking water, it is appropriate now to discuss what is meant by toxicity. The German physician Paracelsus explored the relationship between dose and response. To paraphrase his conclusion: All things are poison and nothing without poison. Solely the dose determines that a thing is not a poison.
The toxicity of a chemical needs to be assessed in a way that relates dose to the receptor, such as an animal or human, and the time of exposure. Criteria, qualitative and quantitative statements of such relationships, are difficult to determine. For example, a high concentration may kill in a short time, but a lower concentration either may be lethal over a longer period than is measured, or may not kill but instead affect the behaviour or the susceptibility to environmental stress cumulatively over the lifetime of the receptor.
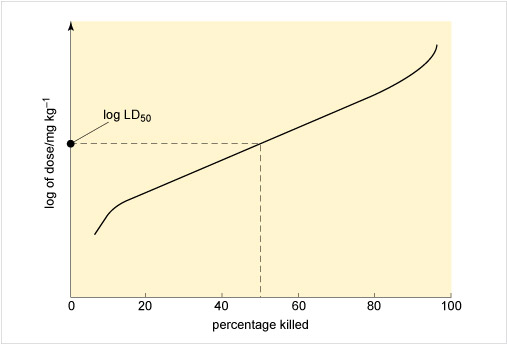
Figure 3 illustrates an approach to assessing toxicity, showing the connection between the dose given and the response to the chemical. This dose-response is measured by the percentage of rats killed by receiving a particular dose, expressed as milligrams per kilogram rat body weight. From this the LD50, the applied lethal dose responsible for killing 50% of the rat population, may be obtained (Table 2 shows some examples).
If the dose is expressed in terms of concentration, it is possible to record the percentage kill after different periods of exposure to varying levels of the chemical. Such a graph can yield the LC50, or median lethal concentration, which is the applied lethal concentration responsible for killing 50% of the rat population when administered as a single exposure.
In the case of the LD50, a distinction is made between short-term and long-term toxic action:
- An acute LD50 is measured after the administration of a single dose.
- A chronic LD50 refers to longer-term exposure following two or more doses given at different times.
- As LC50 values tend to be long-term measurements, they are more comparable to chronic rather than acute LD50 values.
- The effect varies depending upon how the chemical is administered, such as oral versus dermal administration.
A related value that is often quoted is the lethal dose low (LDLO) which is the lowest dose per unit of body weight (typically in mg kg−1) of a chemical known to have produced death in a particular receptor, such as a human or rat.
| LD50/mg kg−1 body weight | Examples | Classification |
|---|---|---|
| less than 25 | arsenic(III) oxide As2O3 | very toxic |
| sodium cyanide NaCN | ||
| thallium(I) sulfate Tl2SO4 | ||
| 25 to 200 | sodium nitrite NaNO2 | toxic |
| sodium fluoride NaF | ||
| 200 to 2000 | arsenic As | harmful |
| sodium nitrate NaNO3 | ||
| aluminium(III) fluoride AlF3 | ||
| indium(III) chloride InCl3 |
Compare: (a) the toxicity of As with As2O3 and (b) the various sodium salts, what does this suggest?
(a) The toxicity of As is lower compared to As2O3 which suggests that the oxidation number, often referred to as the oxidation state of an element, is important.
(b) The higher toxicity of NaCN compared to say NaNO2 suggests that the toxicity is determined by a contribution from each component ion present in an ionic compound, furthermore as this is oral toxicity these compounds will dissociate upon dissolution in the saliva or stomach acids. Indeed cyanide salts are generally very toxic compounds principally due to the cyanide anion.
For most kinds of toxicity, it is generally assumed that there is a dose below which no adverse effects will occur. For chemicals that give rise to known toxicological effects, a tolerable daily intake (TDI), over the whole lifetime without causing harm, can be derived as follows:
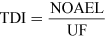
or
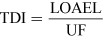
where UF is an uncertainty factor.
The NOAEL, no observable adverse effect level, defines the level of exposure to a chemical at which there is no biologically or statistically significant increase in the frequency or severity of any adverse effects in the exposed population compared with a control group. The closely related LOAEL, lowest observable adverse effect level, is the level where adverse effects are observed.
The guideline value (GV) is then calculated from the TDI as follows:
where bw = body weight, taken as 60 kg for adults, 10 kg for children and 5 kg for infants, p = fraction of the TDI allocated to drinking water, C = daily drinking water consumption (2 litres for adults, 1 litre for children, 0.75 litre for infants).
Toxicological information is usually found within the Materials Safety Data Sheet (MSDS) for commercial chemicals on the websites of chemical suppliers such as Fisher Scientific or Sigma Aldrich.
Problems have historically been reported from drinking well water polluted at 100 mg NO3− per litre. Assume the toxicity is due to the nitrate anion and the oral LDLO for sodium nitrate is 22.5 mg kg−1 for an infant, would a typical infant drink enough polluted water to be in any potential danger? Assume a 5 kg infant as suggested earlier and that an infant normally drinks 150 ml per kg per day.
Assuming 5 kg infant, so LDLO = 22.5 × 5 mg = 112.5 mg of NaNO3.
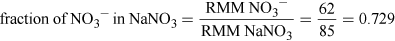(Equation 5)So, NO3− LDLO = 112.5 × 0.729 mg = 82 mg
For polluted water containing NO3− at 100 mg l−1 to reach an LDLO of 82 mg requires drinking water of
(Equation 6)to risk a potentially lethal acute dose.
Normally, an infant drinks 5 × 150 ml per day = 750 ml = 0.75 l.
Therefore, the infant would have been within 10% of a potentially harmful dose. However, Table 1 illustrates that the nitrate concentration is now not observed as high as 100 mg l−1 in the EU countries because the European Commission regulates the maximum amount of nitrate at 50 mg l−1.