4.3 The luminosity of AGNs

It is instructive to express the luminosity of an AGN in terms of the luminosity of a galaxy like our own. The figure may then be converted into solar luminosities, if we adopt the figure of 2 × 10¹⁰L_⨀ for the luminosity of our Galaxy.

Consider a Seyfert galaxy first. At optical wavelengths the point-like AGN is about as bright as the remainder of the galaxy, which radiates mainly at optical wavelengths. But the AGN also emits brightly in the ultraviolet and the infrared, radiating at least three times its optical luminosity. So one concludes that for a typical Seyfert, the AGN has at least four times the luminosity of the rest of the galaxy.

We have seen that a characteristic of a quasar is that its luminous output is dominated by emission from its AGN. However quasar host galaxies are not less luminous than normal galaxies, so the AGNs of quasars must be far brighter than normal galaxies and must also be considerably more luminous than the AGNs of Seyfert galaxies.

In the case of a radio galaxy, the AGN may not emit as much energy in the optical as Seyfert and quasar AGNs, but an analysis of the mechanism by which the lobes shine shows that the power input into the lobes must exceed the luminosity of a normal galaxy by a large factor, and the AGN at the centre is the only plausible candidate for the source of all this energy.

A similar conclusion for AGN luminosity follows for blazars, which appear to be even more luminous than quasars. We examine why in Section 4.7.

Question 8

Calculate the luminosity of an AGN that is at a distance of 200 Mpc, and appears as bright in the optical as a galaxy like our own at a distance of 100 Mpc. Assume that one-fifth of the energy from the AGN is at optical wavelengths.

Answer

The relationship between flux density F, luminosity L and distance d can be given by the following equation:

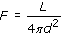
Using this relationship it can be seen that if the AGN is at twice the distance but appears as bright as the normal galaxy in the optical, then it must be emitting four times the optical light of the normal galaxy like our own. If only one-fifth of the AGN's energy is emitted in the optical, then its luminosity is 4 × 5 = 20 times that of the normal galaxy like our own, assuming that (as usual) the normal galaxy emits mostly at optical wavelengths. The AGN luminosity is thus about 20 × 2 × 10¹⁰L_⊙ = 4 × 10¹¹L_⊙.

One can conclude that AGNs in general have luminosities of more than 2 × 10¹⁰L_⊙ produced within a tiny volume. Stop to ponder this statement for a minute. The power output of the Sun is so large that it is hard to comprehend; the number 2 × 10¹⁰ is even more difficult to imagine! Putting together over 2 × 10¹⁰ Suns' worth of luminosity inside an AGN is well beyond the powers of imagination of most of us. One Sun's worth of luminosity is about 4 × 10²⁶ W, so a typical AGN has a luminosity of more than 8 × 10³⁶ W. In fact, that's quite modest for an active galaxy, so for the purposes of this course we shall adopt a more representative value of 10³⁸ W as the characteristic luminosity of an AGN.

You are now in a position to appreciate the basic problem in accounting for an AGN. It produces an enormous amount of power (luminosity) in what is astronomically speaking a tiny volume. This source of power is known as the engine. Current ideas about the workings of this engine are discussed in the next section.