4.5 An accretion disc

What will happen to matter that comes near a black hole? Consider a gas cloud moving to one side of the black hole, such as cloud A in Figure 29.

Figure 29: Schematic diagram of discrete gas clouds falling towards a black hole. Clouds C and D are shown colliding. This will allow the clouds to become trapped in an orbit around the black hole

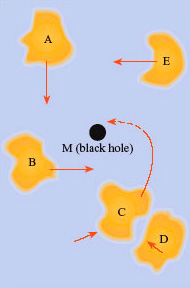
The hole's gravity will accelerate the gas cloud towards it. The cloud will reach its maximum speed when it is at its closest approach to the black hole, but will slow down again as it moves away; it will then move away to a distance at least as great as the distance from which it started. Thus far nothing is new; the gas cloud will behave exactly as it would if it came near some other gravitationally attracting object, such as a Sun-like star.

Now, let us extend the argument to a number of gas clouds being accelerated towards the black hole from different directions in space. This time, as the gas clouds get to their closest approach they will collide with each other, thus losing some of the kinetic energy they had gained as they fell towards the hole. Therefore some, but not all, of the clouds of gas will have slowed to a speed at which they cannot retreat, so they will go into an orbit around the hole. Further collisions amongst the gas clouds will tend to make their orbits circular, and the direction of rotation will be decided by the initial rotation direction of the majority of the gas clouds. The effect of the collisions will be to heat up the gas clouds; the kinetic energy they have lost will have been converted into thermal energy within each cloud, and so the cloud temperature will rise.

So far, we can envisage a group of warm gas clouds in a circular orbit about the black hole. But the clouds of gas are of a finite size and, because they move in a Keplerian orbit, the inner parts of the gas clouds will orbit faster than the outer parts. A form of friction (viscosity) will act between neighbouring clouds at different radii and they will lose energy in the form of heat. The consequence of this is that the inner parts of the gas clouds will fall inwards to even smaller orbits. This process will continue until a complete accretion disc is formed around the black hole (Figure 30).

Figure 30: A rotating accretion disc; the line shows the spiral infall of one particle

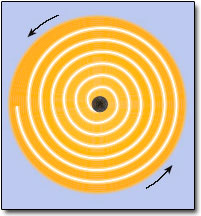
The accretion disc acts to remove angular momentum from most of the gas in the disc so that if you look at the path of a small part of one gas cloud, you can see that it will spiral inwards. Since angular momentum is a conserved quantity the accretion disc does not actually diminish the total angular momentum of the system - it simply redistributes it such that most gas in the disc will move inwards. This process occurs only for a viscous gas - planets in the Solar System do not show any tendency to spiral in to the Sun because interplanetary gas is very sparse. The viscosity causes the gas to heat up further, the thermal energy coming from the gravitational energy that was converted into kinetic energy as the gas fell towards the hole. The heating effect will be large for objects with a large gravitational field and so we might expect that accretion discs around black holes will reach high temperatures and become luminous sources of electromagnetic radiation.

The gradual spiralling-in of gas through the accretion disc comes to an abrupt end at a distance of a few (up to about five) Schwarzschild radii from the centre of the black hole. At this point the infalling material begins to fall rapidly and quickly passes through the Schwarzschild radius and into the black hole. Note that the accretion disc is located outside the event horizon, where the heat can be radiated away as electromagnetic radiation. The accretion model is of such interest because an accretion disc around a massive black hole can radiate away a vast amount of energy, very much more than a star or a cluster of stars. It is this radiated energy that is believed to constitute the power of an AGN.

You may be wondering how large the accretion disc is; after all, the accretion disc as well as the black hole has to fit inside the AGN. The accretion disc gets hotter and therefore brighter towards its inner edge. The brightest, and hence innermost part is what matters. Since this is at only a few times the Schwarzschild radius, there is no problem of size.

• Estimate the extent of the brightest part of the accretion disc for a black hole of mass 10⁸M_⊙. How does this compare with the radii of planetary orbits in the Solar System?

• From Section 4.4 we know that the Schwarzschild radius is about 3 × 10¹¹ m, which is twice the radius of the Earth's orbit or 2 AU. The brightest part of the accretion disc could then extend to about five times this distance or about 10 AU, which is about the radius of Saturn's orbit.