Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Electronic applications
Electronic applications

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3.5 Digital filtering in the time domain

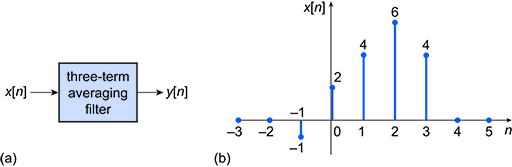
A simple form of digital filter is the three-term averaging filter, in which the output value is equal to the average of three successive signal sample values. In Figure 19(a), which shows a discrete-time signal applied to a digital three-term averaging filter, the output y of n is given by

y of n equals sum with, 3 , summands one divided by three times x of n plus one divided by three times x of n minus one plus one divided by three times x of n minus two

The signals x of n and x of n minus one are spaced cap t seconds apart in time, where cap t is the sampling interval. Similarly, x of n minus one and x of n minus two are spaced cap t seconds apart.

Figure 19(b) shows the values of the input signal x of n that will be applied to the filter input.

Described image
Figure 19 (a) Three-term averaging filter; (b) input signal to the three-term averaging filter
Show description|Hide description

This figure consists of two parts.

Part (a) is a simple block diagram showing a three-term averaging filter with input x[n] and output y[n].

Part (b) is a graph of x[n] against n. Input samples x[n], represented as usual as vertical lines extending from the horizontal axis with filled circles at the end, are shown for integer values of n from minus 3 to 5. The values are as follows:

  • when n is minus 3, x[n] is 0

  • when n is minus 2, x[n] is 0

  • when n is minus 1, x[n] is minus 1

  • when n is 0, x[n] is 2

  • when n is 1, x[n] is 4

  • when n is 2, x[n] is 6

  • when n is 3, x[n] is 4

  • when n is 4, x[n] is 0

  • when n is 5, x[n] is 0.

Figure 19 (a) Three-term averaging filter; (b) input signal to the three-term averaging filter

The values of n and x of n are listed in Table 1. Assume that x of n equals zero for any n less than negative three and n greater than five.

Table 1  Values of n and x of n from Figure 19(b)
n −3 −2 −1 0 1 2 3 4 5
x of n   0   0 −1 2 4 6 4 0 0

For the output y of n to be calculated, the values of x of n, x of n minus one and x of n minus two must be stored in memory and accessible to the processor performing the calculation. The order of a digital filter is the number of previous inputs (stored in the processor’s memory) used to calculate the current output, so this three-term averaging filter is second-order.

For values of n less than negative one the output will be 0, so the calculations below start at n equals negative one.

For n equals negative one you can substitute in values to give equation sequence y of negative one equals one divided by three multiplication open negative one close plus one divided by three multiplication zero plus one divided by three multiplication zero equals negative one divided by three.

For n equals zero you get y of zero equals one divided by three multiplication two plus one divided by three multiplication open negative one close plus one divided by three multiplication zero postfix times equation left hand side equals right hand side one divided by three.

For n equals one you get y of one equals one divided by three multiplication four plus one divided by three multiplication two plus one divided by three multiplication open negative one close postfix times equation left hand side equals right hand side five divided by three.

Table 2 shows the results of all calculations for y of n, shown as decimal values to 2 significant figures. Note that you can stop at n equals five, since above this the output will be 0 again.

Table 2  Results of calculations for y of n
n −3 −2 −1 0 1 2 3 4 5
x of n   0   0 −1 2 4 6 4 0 0
y of n   0   0 −0.33 0.33 1.67 4.00 4.67 3.33 1.33

The resulting output discrete-time waveform is given in Figure 20.

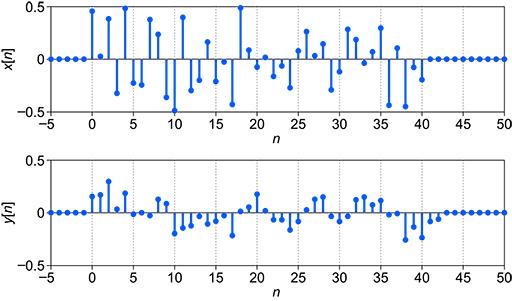
Described image
Figure 20 Filter output in response to the input in Figure 19(b)
Show description|Hide description

This figure is a graph of y[n] against n. Output samples y[n], represented as usual as vertical lines extending from the horizontal axis with filled circles at the end, are shown for integer values of n from minus 3 to 5. The values are as follows:

  • when n is minus 3, y[n] is 0

  • when n is minus 2, y[n] is 0

  • when n is minus 1, y[n] is minus 0.33

  • when n is 0, y[n] is 0.33

  • when n is 1, y[n] is 1.67

  • when n is 2, y[n] is 4

  • when n is 3, y[n] is 4.67

  • when n is 4, y[n] is 3.33

  • when n is 5, y[n] is 1.33.

A note states that the output values are zero beyond n equals 5.

Figure 20 Filter output in response to the input in Figure 19(b)

Figure 21 shows the same filter applied to an input x of n that has more noise in the signal and a longer sequence.

Described image
Figure 21 Longer sequence filtered by the three-term averaging filter (Wickert, 2011, p. 7)
Show description|Hide description

This figure consists of two graphs. In each case, the signal values are represented as vertical lines extending from the horizontal axis with filled circles at the end, and can take any value from minus 0.5 to 0.5. They are shown for integer values of n from minus 5 to 50.

The first graph is x[n] against n. The input values x[n] vary from one to the next by quite large amounts.

The second graph is y[n] against n. The output values y[n] vary less from one to the next; they appear to follow the same overall shape as the input values, but more smoothly and with less extreme values (the largest value is approximately 0.3 in magnitude, rather than 0.5).

For example, on the input graph, the first five values are 0, the sixth is nearly 0.5, the seventh is close to 0 again, the eighth is about 0.4, the ninth is about minus 0.3, and the tenth is 0.5. On the output graph, the first five values are 0, the sixth and seventh are about 0.2, the eighth is about 0.3, the ninth is just above 0, and the tenth is just above 0.2.

Figure 21 Longer sequence filtered by the three-term averaging filter (Wickert, 2011, p. 7)

Activity 8

Timing: Allow about 5 minutes

Looking at Figure 21, describe the effect that the three-term averaging filter has on the output. What kind of filter is this?

Answer

The three-term averaging filter has removed the short-term fluctuations in the signal to show the longer-term trend. This is akin to removing higher-frequency noise from a signal, so it is operating like a low-pass filter.

This digital filter is an example of a system that is both linear and time-invariant, sometimes referred to as an LTI system.

You can see that the three-term averaging filter is a low-pass filter, but it is difficult to characterise its response. For example, what frequencies is the filter eliminating from the signal? Earlier in this course, you saw how analogue filters can be designed to give a desired frequency response; now you will look at how digital filters can also be designed in the frequency domain.

Filters are usually described in terms that make sense in the frequency domain, e.g. a low pass filter allows the parts of the signal with low frequencies to pass. In the following section you will see how a digital filter is designed in the frequency domain.