3.1 Vector addition in component form

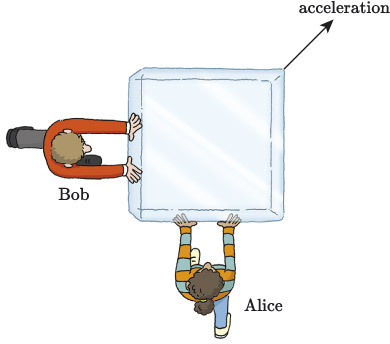
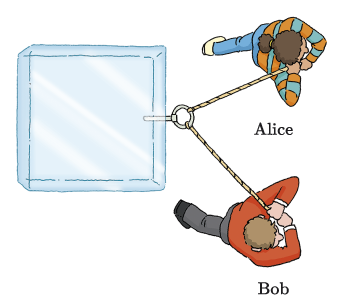
Let’s return to Alice and Bob pushing a block of ice, with each pushing on a different face of the block, as illustrated in Figure 22. If Bob applies a force of 130 N to the left face of the block, and Alice applies a force of 110 N to the bottom face, what is the combined force applied to the block?

Figure 22 Alice and Bob pushing different sides of a block of ice

Show description|Hide description

Alice and Bob pushing different sides of a block of ice. Alice is pushing the block forwards whilst Bob is pushing the Block to the right. These two actions result in the block accelerating diagonally.

Figure 22 Alice and Bob pushing different sides of a block of ice

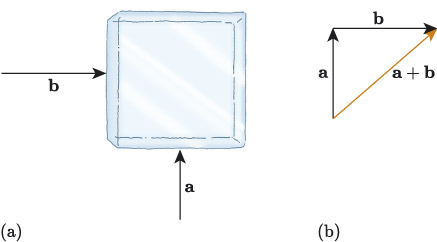
Figure 23(a) shows an abstraction of the drawing in Figure 22. Here, represents the force applied by Alice, who is below the block, and represents the force applied by Bob, who is to the left of the block.

Figure 23 Combining the vectors and

Show description|Hide description

23(a): Vector a is the block moving forward whilst vector b is the block being pushed to the right.

23(b): These two vectors can be combined and give the resultant vector a+b.

Figure 23 Combining the vectors MathJax failure: MathML - Unexpected text node: '

Vector is a vertical vector so its -component is zero, and is a horizontal vector so its -component is zero. Together, and are the horizontal and vertical components of the resultant vector , so we can say that

So the net force on the block of ice in Figure 22 is represented by the vector .

This example was straightforward because we were considering perpendicular forces acting vertically and horizontally. But the process we followed is the same for any vector addition. Using the component form of two vectors  and , we add them together algebraically to determine the resultant vector .

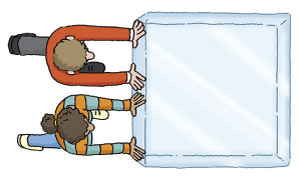
Let’s consider another example. In Figure 24, Alice and Bob are both pushing the same face of the block of ice. If, as before, Bob applies a force of 130 N and Alice a force of 110 N, what is the combined force applied to the block?

Figure 24 Alice and Bob pushing a block of ice

Show description|Hide description

Alice and Bob push on the same side of a block of ice so that it moves to the right.

Figure 24 Alice and Bob pushing a block of ice

Again we let the vector represent the force applied by Alice and vector represent the force applied by Bob, so this time and are both horizontal vectors.

Both vectors act horizontally, so are acting in the same direction, the direction of the positive -axis, and we’d expect them to add up with the net result being a stronger force acting in the same direction. If we add the component forms of and , then this is the result we get:

So the resultant vector is , and the net effect is a force of 240 N acting in the direction of the positive -axis. The resultant force on the block of ice is the sum of the forces applied by Alice and Bob, and the block will accelerate faster in the direction they are pushing as we’d intuitively expect.

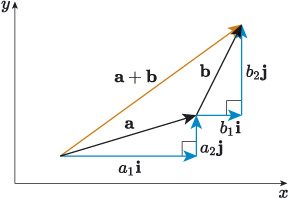
To summarise, when we add vectors in component form, we add the individual components. This is illustrated visually in Figure 25, where the vector is the sum of the two vectors and , and the components of are the sums of the individual components of and . So expressing in component form gives us the following.

Figure 25 Sum of the vectors and

Show description|Hide description

Vector a travels in one direction before changing to a direction denoted as vector b where a = a1i + a2j and b = b1i + b2j. The resultant vector is given as the sum of the two vectors a+b.

Figure 25 Sum of the vectors MathJax failure: MathML - Unexpected text node: '

For example, the sum of the vectors and is given by

We can also add the vectors using column form. For example:

This method of adding vectors also extends to sums of more than two vectors. For example, if , and , then

Using component vectors we can add vector quantities algebraically. Let’s reconsider our block of ice example where Alice and Bob are both pulling the block in different directions (see Section 1.2). Using the component form of vectors, we can quickly calculate the combined force applied by Alice and Bob to the block of ice.

Example 3 Calculating the magnitude of combined forces

Alice and Bob have attached ropes to a face of the block of ice and are pulling it in different directions, see Figure 26. Bob pulls with a force of 130 N at an angle of 47° clockwise from the horizontal, and Alice pulls with a force of 110 N at an angle of 24° anticlockwise from the horizontal. Express the forces applied by Alice and Bob in component form, and use these to determine the magnitude of the combined force applied to the block.

Figure 26 Alice and Bob pulling on a block of ice in different directions

Show description|Hide description

Alice and Bob pull on the same side of a block of ice but in different directions.

Figure 26 Alice and Bob pulling on a block of ice in different directions

Solution

First let’s express the forces applied by Alice and Bob in component form.

Alice applies a force with magnitude 110 N at an angle of 24°. So in component form we have

Bob applies a force with magnitude 130 N at an angle of 360° – 47° = 313°. So in component form we have

To calculate the combined force, add the corresponding components:

So the magnitude of the combined force is