Solutions to activities

Activity 1

is the hypotenuse of the right-angled triangle formed by , and the resultant , so from Pythagoras’ theorem its magnitude is given by

This gives

So the magnitude of is 170.29 (to 2 d.p.).

Activity 2

Angles and are alternate angles, so they are equal. We can find using the tangent function, which is given by

So

therefore

This gives (to 1 d.p.) and this is the direction of the vector .

Activity 3

• a.After 30 seconds we have

  and

  So the block is travelling at a speed of approximately and has travelled a distance of approximately 76.5 m.

• b.After 60 seconds we have

  and

  So the block is travelling at a speed of approximately and has travelled a distance of approximately 306 m.

Activity 4

First we need to determine the size of angle . We can use the angles 24° and 47° to calculate because they sit on the same straight line as , so

Now, using the cosine rule, we can calculate the length of edge :

So

Activity 5

Using the sine rule, we get

so

Using the inverse sine function, we get

Activity 6

Newton’s second law gives

so acceleration is given by

therefore

The direction of the acceleration is the same as the direction of , and this is measured clockwise from the positive -axis.

The magnitude of the acceleration is

So the block accelerates at (to 2 d.p.) in a direction that is measured clockwise from the positive -axis.

Activity 7

The magnitude of the vertical component is given by

so

The magnitude of the horizontal component is given by

so

Activity 8

The horizontal displacement is and the vertical displacement is , so .

The horizontal displacement is and the vertical displacement is , so .

The horiztonal displacment is and the vertical displacement is , so .

Activity 9

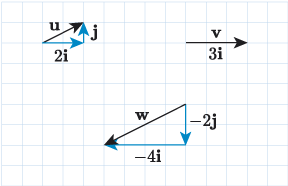
Activity 10

• a.The component form of the vector is given by

• b.The component form of the vector is given by

Activity 11

• a.The magnitude of is

  and the direction is given by

  The calculator value for is , but looking at a drawing of the vector below, shows that this is not the correct angle. Instead, we are looking for a value of that is greater than and less than .

  

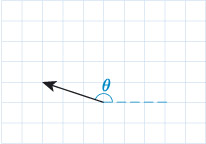
  By considering the graph of , we can identify the angles that are within the range, and using the periodicity of the tangent function we can say that the value for is

• b.The vector has no vertical component, and a negative horizontal component. So it points in the negative -direction and its magnitude is

• c.The magnitude of is

  and the direction is given by

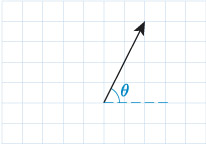
  The calculator value for is . Looking at a drawing of the vector below shows that this is the correct value for , because it is greater than and less than .

  

Activity 12

Activity 13

and .

Activity 14

• a.

• b.

• c.

Activity 15

• a.

• b.

• c.

• d.

• e.

• f.

Activity 16

• a.

• b.
• c.

Activity 17

• a.

• b.

• c.

Activity 18

• a.

• b.Rearranging gives

  So .

Activity 19

• a.

• b.

• c.

Activity 20

• a.

• b.

• c.

Activity 21

Expand the brackets by using property 4:

Simplify by using property 3 to give

Simplify further by using property 2:

Activity 22

First let’s use the components of and to find , and . We have

Using these we can calculate :

So

The angle between the vectors is 27° (to the nearest degree).