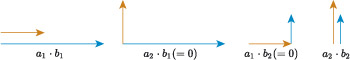4.1 Scalar product of a vector from components

Consider vectors and in Figure 29. In component form these are written as and . How can we calculate the scalar product ?

Figure 29 Finding the scalar product of and by comparing components

Show description|Hide description

Finding the scalar product of two vectors, a and b. a is made up of components a1i and a2j whilst b has components b1i and b2j. The scalar product is given by a · b.

Figure 29 Finding the scalar product of MathJax failure: MathML - Unexpected text node: '

The scalar product will tell us how much vector will grow vector , and to determine this we want to identify how much the vectors interact. One method is to consider how much the horizontal and vertical components of the vectors interact, as illustrated in Figure 30. There are four possible combinations to consider: horizontal to horizontal, horizontal to vertical, vertical to horizontal, and vertical to vertical.

Maximise

Figure 30 Interacting component vectors in the scalar product of and

Show description|Hide description

Interacting component vectors in the scalar product of a and b. The i component is given by a1 · b1 and the j component is given by a2 · b2. When a and b are perpendicular, the scalar product is 0.

Figure 30 Interacting component vectors in the scalar product of MathJax failure: MathML - Unexpected text node: '

Horizontal components do not interact with vertical components (and vice versa) because they are independent of each other, so and , and they do not contribute to the value of scalar product. Horizontal components interact with each other, and vertical components interact with each other, so and both contribute to the value of .

The expression is a measure of how much the scalar quantity grows the scalar quantity , so it is equal to , and similarly is equal to . The scalar product is a combination of these, so

For example, if and , then