2.2 Cartesian unit vectors
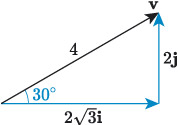
In Activity 7 we found that the vector has a vertical component with a magnitude of 2 and a horizontal component with a magnitude of . So we can write
The vector and its horizontal and vertical components form a triangle, as illustrated in Figure 14, and we discovered in Chapter 1 that vector sums form triangles. So this equation makes sense mathematically, and it is correct to say that a vector is the sum of its horizontal and vertical components.
A shorthand way to write this is
The vectors and are called the Cartesian unit vectors. Here, unit means one, so and are vectors with magnitude 1 that point in the directions of the coordinate axes. The unit vector points in the direction of the -axis and, similarly, the unit vector points in the direction of the -axis, as illustrated in Figure 15(a).
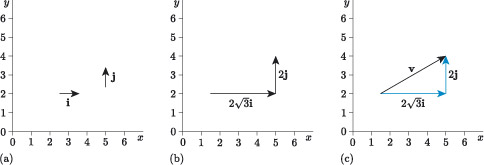
Consider what the expression means. We are multiplying the unit vectors and by scalar values and , as illustrated in Figure 15(b). Using the rule for multiplying a vector by a scalar:
- multiplying by gives a vector of magnitude pointing in the direction of the positive -axis
- multiplying by gives a vector of magnitude pointing in the direction of the positive -axis.
So is a quick way to write ‘horizontal component of magnitude ’, and is a quick way to write ‘vertical component of magnitude ’, and the sum of these is the vector , as illustrated in Figure 4.15(c).
Expressing a vector as the sum of scalar multiples of unit vectors is a useful shorthand, and every vector can be described in this way. It works because perpendicular vectors act independently from each other – a change in the horizontal component has no effect on the vertical component, and vice versa. This is also what happens in the physical phenomena that are modelled using vector quantities, such as motion.
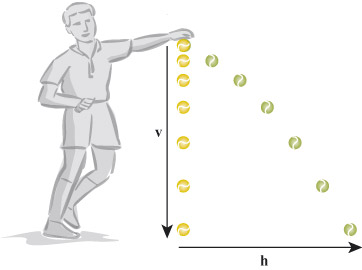
Imagine you have two balls, ball A and ball B, and you throw ball A forward at the same time that you drop ball B, as illustrated in Figure 16. Now, consider the velocities of the two balls. For both balls a vertical velocity is produced as a consequence of weight due to gravity. For ball A there is also a horizontal velocity because it has been thrown forward. Which ball do you expect will hit the ground first?
You may be surprised to hear that both balls will hit the ground at the same time. This is because, regardless of how fast ball A is thrown forward, the horizontal velocity has no effect on the vertical velocity – the vectors are independent because they are perpendicular.
Component form of a vector
If , then the expression is called the component form of . The scalar is called the -component of and the scalar is called the -component of .
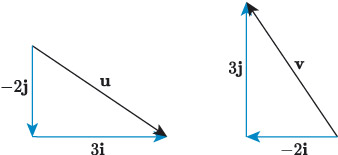
Recall, from Chapter 1, that it is convention that if the horizontal component of a vector points in the direction of the negative -axis, then its magnitude is negative, and similarly if the vertical component points in the direction of the negative -axis, then its magnitude is negative. For example, in Figure 17 the component form of vector is , so its -component is and its -component is . Similarly, the component form of the vector is , so its -component is and its -component is .
Sometimes, the - and -components of a two-dimensional vector are called the - and -components.
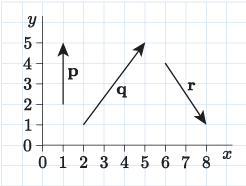
Activity 8
Express the following vectors , and in component form.
An alternative way for expressing a vector in component form is the column vector, which is common in engineering.
This is a column of numbers surrounded by brackets, where the first number is the -component and the second number is the -component. For example,
Both ways of expressing the vector are equally valid, but column vectors are often preferred because there is no need to explicitly write the and . It is often the convention that the components of a vector are expressed using the same letter as the vector (but not bold or underlined), with subscripts. For example,
Alternative component form of a vector
The vector can be written as .
A vector written in this form is called a column vector.
Activity 9
Use your own grid and draw the following vectors.