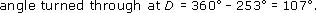1.3.2 Angles on a line
If several angles make up a half turn, then the sum of those angles must be 
× 360° = 180°. Therefore, in the following diagram, α + β + γ + δ = 180°.
The sum of angles on a line is 180°.
(Note that different diagrams can be labelled with the same letters – α, β, γ, and δ in this case. The letters represent different angles here to those in the diagram in the preceding section.)
You can sometimes use these properties to determine unknown angles.
Example 2
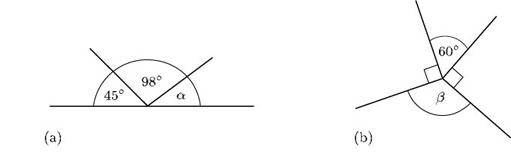
Find α and β in the diagrams below. These are the types of diagram that might arise when plotting the course of a ship.
Answer
(a) As the angles are on a line,
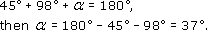
(b) As the angles are at a point,
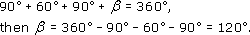
Example 3
Students at an orienteering event follow a route round a set course in a clockwise direction. (Assume that the students run in straight lines and keep to the track.)
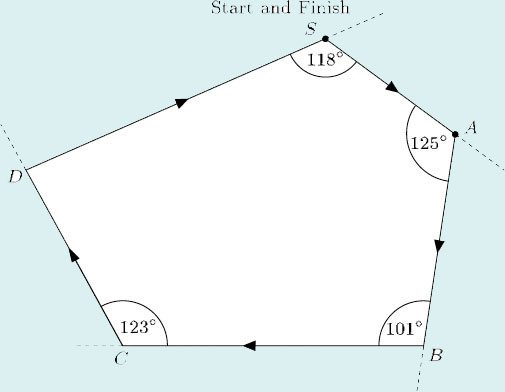
(a) Through what angle do the students turn at A?
(b) When they arrive at D, what is the total angle that they have turned through relative to their starting direction?
(c) When they return to S, through what angle must they turn in order to face in the direction in which they started?
(d) When they reach D, through what angle must they turn in order to return to the start?
Answer
(a) The angle turned through at A is 180° − 125° = 55°.
(b) The angle turned through at B is 180° − 101° = 79°, and the angle turned through at C is 180° − 123° = 57°.
So the total angle that the students have turned through when they arrive at D is 55° + 79° + 57° = 191°.
(c) The angle that the students need to turn through at S is 180° - 118° = 62°.
(d) Suppose the students complete the whole course and, at the finish, face in the same direction as at the start, they will overall have made one complete turn, that is, 360°.
So
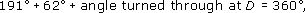
hence
