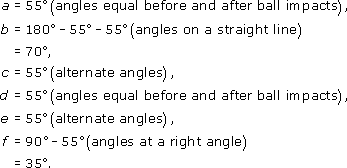Try some yourself
Question 1
Find α and β in each of the diagrams below.
Answer
(a) Now 
so 
But 
so 
Question 2
Answer
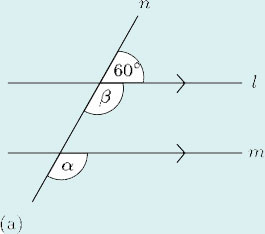
(b)
There are many ways of finding the sizes of these angles. This is only one of them:
As 
it follows that 
But 
so 
Similarly, 
so 
But 
so 
Question 3
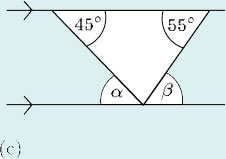
Answer
(c) α = 45° (alternate angles).
β = 55° (alternate angles).
Question 4
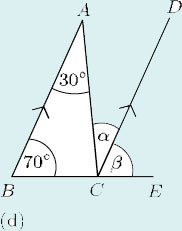
Answer
(d) α = 
= 30° (alternate angles).
β = 
= 70° (corresponding angles).
Question 5
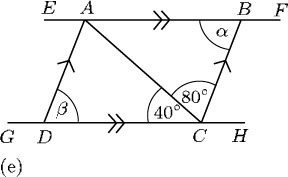
Answer
(e) As 
it follows that 
But β and 
are corresponding angles, so
Whereas α and are alternate angles, so 
Question 6
2 This diagram shows part of some bannister rails. The handrail makes an angle of 40° with the horizontal. Calculate angles α, β, γ and δ.
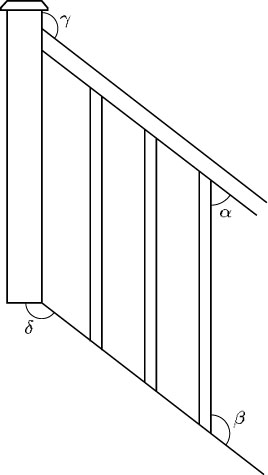
Answer
It is a good idea to sketch a diagram, adding some horizontal lines where necessary.
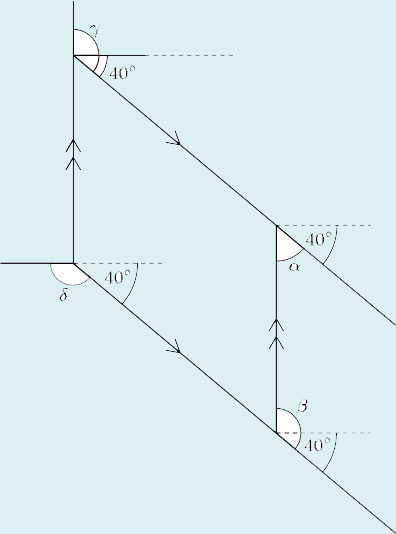
Assume the lines marked are pairs of parallel lines. Then, since the handrail makes an angle of 40° with the horizontal,
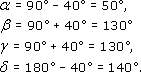
Question 7
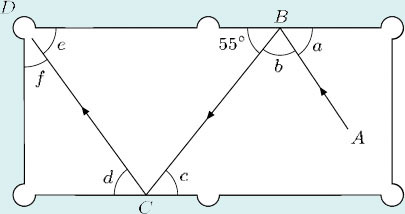
3 The arrows on the diagram below indicate the idealised path (ABCD) of a snooker ball on a snooker table. Assume that the angles between the cushion (the edge of the snooker table) and the path of the ball before and after it impacts with the cushion are equal. Calculate the sizes of the angles marked a, b, c, d, e and f.
Answer
