1.2.4 Ammonia synthesis by bulk production

To make high explosives, such as TNT, requires chemicals called 'nitrates'. At the time of the First World War these were obtained from a natural mineral, which was mostly supplied from South America. Germany was cut off from these mineral supplies, so its chemical industry was charged with the task of manufacturing nitrates artificially.

Nitrates are essentially composed of two gaseous elements: nitrogen and oxygen, which are chemically combined. Nitrogen is abundant in the atmosphere, around 76% by mass, but in an unreactive form. The task therefore came down to coaxing atmospheric nitrogen into a more reactive condition. A particularly good method of achieving this is to combine nitrogen with another gaseous element, hydrogen, to form ammonia. The Haber–Bosch process for making ammonia was the outcome of the German war-driven research and enabled Germany to maintain its supplies of munitions. The process is now the mainstay of ammonia production world-wide each year, with ammonia mainly used as the basis of nitrogenous fertiliser. That said, it is also used as a constituent of many household cleaners, as a refrigerant in industrial refrigeration systems, to scrub sulphur dioxide from the burning fossil fuels used in power plants, and for the pulping of wood in the paper industry (Figure 12).

Maximise

Figure 12 Uses for ammonia: (a) household cleaner; (b) fertiliser; (c) ice rink refrigeration; (d) scrubbing in coal-fired power stations; (e) production of wood pulp

Show description|Hide description

Figure 12 is an array of 5 photographs. Reading left to right, top to bottom, the first image shows cleaning materials (rubber gloves, sponges and a hand-held spray dispenser) on a tiled floor. The next image shows a farm tractor pulling a fertilizer spreader across a crop field. The next image shows an ice rink being used for a game of ice hockey. The next picture shows a view of a power station identified as such by the row of cooling towers with steam coming from them and two taller chimneys with smoke coming from them. The final image is a close up photograph of a bale of wood pulp.

Figure 12 Uses for ammonia: (a) household cleaner; (b) fertiliser; (c) ice rink refrigeration; (d) scrubbing in coal-fired power ...

Activity 5 (video)

Watch Video 1 which describes the background to the discovery of how to manufacture ammonia artificially.

Download this video clip.Video player: Video 1 Manufacturing ammonia artificially (2 minutes)

Show transcript|Hide transcript

Transcript: Video 1 Manufacturing ammonia artificially (2 minutes)

NARRATOR:

100 years ago, rapidly growing populations put pressure on farmers to grow more food. The traditional fertiliser, animal manure, wasn't enough. The one good source of the nitrates they needed was 8,000 miles away in Chile.

Guano, seabird droppings accumulated over thousands of years, were mined and shipped to Europe. And the reserves were running out. To the rescue came a German chemist. Like a latter day alchemist, Fritz Haber achieved a seemingly magical transformation. He fused nitrogen from the air and hydrogen from hot coke and steam and, hey, presto, ammonia, from which nitrates could easily be made. A saviour of the planet? Well, nothing's quite that simple.

Germany's ability to synthesise ammonia took on a new significance as the first world war began. Their sea routes to the vital Chilean guano were cut just as their explosives industry was demanding more and more of the material. Their front line guns were fed by a harbor's brainchild, conjured from air and water.

End transcript: Video 1 Manufacturing ammonia artificially (2 minutes)

Download

Video 1 Manufacturing ammonia artificially (2 minutes)

Interactive feature not available in single page view (see it in standard view).

The production of a chemical like ammonia is rather different from the mass production used for a ballpoint pen. This is because the product, ammonia, is not particularly useful in itself: it becomes the starting material in yet further processes. The product does not come out as discrete items, and production may be continuous. This type of production is often referred to as 'bulk production'.

Ammonia production is a good example of engineering as the 'appliance of science', the science in this case being chemistry (see Engineering with atoms ).

Engineering with atoms

When chemistry is applied as a means to an end, where that end is a product with a function, it can be thought of as engineering with atoms. Clearly chemistry is large-scale engineering, and not one atom at a time. The chemical reactions involved often progress without any intervention from humans, indeed some reactions can only be prevented by ensuring that the chemicals involved are kept well apart. However, there is still engineering skill required for chemical manufacture, such as creating the ideal conditions for bringing atoms together to produce the required product, be it a drug, a fertiliser or furniture polish.

True 'atomic engineering' is beginning to emerge in the field of nanotechnology, where atoms and molecules are manipulated singly, in small groups, or in layers a few atoms thick. Many products are coated with thin films for special purposes. One can think of examples such as the anti-reflective coatings on lenses, hard coatings of titanium nitride on drill bits, and self-cleaning glass windows. These are coated with a very thin layer of titanium dioxide that breaks down dirt particles with the help of sunlight and the oxygen in the air, and have been available to consumers since the early 2000s.

Manipulating atoms one by one takes this a step further, and the ability to do this is especially interesting to computer chip manufacturers. In February 2012, a group of researchers at the University of New South Wales announced that they had made a transistor consisting of a single atom of phosphorus. (A transistor is a device used for amplifying and switching electronic signals.) Figure 13 shows the transistor sitting in the space created by removing an atom of silicon from the surface of a silicon crystal. The two wide bands running diagonally across the image are the electrodes; the gap between them, where the phosphorus atom sits, is 20 nanometres wide. This particular transistor would be difficult to use as it behaves well only if cooled to −233 °C, about 40 K above absolute zero, but the ability to create this device will undoubtedly lead to more practical applications.

Figure 13 A single atom of phosphorus has been placed between two electrodes on a silicon surface, which then acts as a transistor

Show description|Hide description

Figure 13 may be a photograph or a 3D computer model but it is clearly intended to represent the microscopic world. A square piece of silicon is shown as a ridged but otherwise flat surface that is lightly covered in small specks of other substances. The two electrodes are shown as additional substantial lines of material on the surface, starting at opposite corners and laid out along a common diagonal line. They are not long enough to meet and in the middle of the gap between them there is a single atom of phosphorus.

Figure 13 A single atom of phosphorus has been placed between two electrodes on a silicon surface, which then acts as a transistor

For the production of ammonia, the elements nitrogen and hydrogen have to be coaxed to react together: ammonia is the product of this reaction under the right conditions. The right proportions are also needed: 1000 kg of ammonia requires 820 kg of nitrogen to react with 180 kg of hydrogen (see Units of mass ). The reactants (i.e. the chemicals that are reacting) are gases, and so is the product. So one constraint on the production system is that it has to supply the ingredients and remove the product in the gaseous state.

Units of mass

Before defining the units of mass it's very important that the distinction between 'mass' and 'weight' is clear. In everyday language we use the term 'weight' when we're really talking about mass.

For example, many people are interested in their body mass index as a measure of health. When I visit my doctor she asks me to stand on the scales (Figure 14) so that she can 'weigh' me. The reading from the scales is 72 kilograms (kg). To calculate my body mass index my doctor also needs to know my height in metres, which is 1.74 m.

Figure 14 Standing on the scales

Show description|Hide description

Figure 14 is a photograph of someone standing on platform weighing scales. Only the feet of the person are shown in the picture. The scales have a flat surface on which to stand and a large round instrument face with a pointer that rotates when the person stands on the platform. The face has two scales. The inner scale is graduated in kilograms and the outer scale is graduated in stones. The position on the scales where the pointer stops indicates the mass in either kilograms or stones.

Figure 14 Standing on the scales

Now, when my doctor wants to find my body mass index (BMI), she does the following calculation

Fortunately, this is in the healthy range of 20–25.

You may be wondering why I have put 'weight' in inverted commas and why BMI isn't referred to as 'body weight index'. Well, what my doctor is interested in when I stand on the scales is how much of me there is – that is, my mass. And in SI units we measure mass in kilograms. So, the equation should say

But what the scales are actually doing is measuring the force my body exerts on the scales when I stand on them. This force is produced by the gravitational effect of the Earth pulling on my body and this, in engineering terms, is my weight. Weight is measured in 'newtons' however, the scales are calibrated to give a read out in kilograms.

If my doctor and I were on the Moon, where the effect of gravity is much less than it is on Earth, the force that my body exerts on the scales would be less and my weight would be lower. But my mass would not change – there would still be the same amount of me!

The basic unit of mass is the gram, but it is actually the kilogram (1000 grams) that is standardised and which provides the SI unit for mass. A litre of pure water was defined to have a mass of 1 kilogram. Again the definition was translated into a single prototype, this time as a cylinder of a platinum–iridium alloy, which is dense and uncorrodable. The standard kilogram is actually quite a small cylinder (Figure 15), about 4 cm high and wide, housed in an environmentally controlled safe at the BIPM (the International Bureau of Weights and Measures) in Paris.

Figure 15 The standard kilogram

Show description|Hide description

Figure 15 is a photograph of the standard kilogram cylinder housed in a small glass bell jar. Covering this bell jar is another larger glass bell jar and covering that bell jar is another even larger glass bell jar. On the top of the largest external bell jar there is a tap and tube connection, used presumably to alter the atmosphere in the jars once they have been placed in position over the standard. Shown next to the jars is a pair of tongs designed for picking up the kilogram cylinder thereby avoiding contact by human hand, which could possibly alter the mass of the cylinder.

Figure 15 The standard kilogram

Once again – as with length – multiples and subdivisions of the basic unit, the gram, are useful; and, because the SI generally uses a factor of 1000 to define multiples and subdivisions, the prefixes that you met in connection with length are also used with mass.

Table 3 SI units of mass

	Factor	Symbol
microgram	× 1/1 000 000	μg
milligram	× 1/1000	mg
gram	1	g
kilogram	× 1000	kg
tonne	× 1 000 000	t

Notice that 1000 kg (a megagram) is actually called a tonne. (Its spelling distinguishes it from the imperial 'ton', though they are very close – to within about 2%. The imperial system of units is discussed further later in this section.)

You will find examples of SI units of mass in everyday situations, often in combination with other units. Listen out for figures describing air pollution in micrograms per cubic metre (μg m ⁻³ ). The legal limit (in 2012 in the UK) for the concentration of alcohol in a driver's blood is 80 mg per 100 cm ³. Chocolate is often sold in bars of 100 g and sugar in 1 kg bags.

Theoretical chemistry provides us with a clear understanding of what conditions are needed to produce ammonia. There is no need to go into great detail here regarding the chemical principles involved, but it is worth looking at their consequences as an example of the fundamental physical laws that constrain much of engineering. Making ammonia is not as simple as stirring the raw materials together in a bucket; and understanding the process by which ammonia is formed allows us to make it as efficiently as possible.

First, the reaction between nitrogen and hydrogen proceeds better at high pressures. If the engineer can provide a high-pressure system for making the ammonia, it will be much more efficient, and so more productive, than one operating at normal atmospheric pressure.

Secondly, chemical reactions often produce heat, and the formation of ammonia certainly does this. However, if the temperature becomes too high, the reaction can become slow; so the engineer can help production by getting rid of the heat generated by the reaction, thereby keeping production high.

Thirdly, it's important to extract the ammonia as it is being made. As more and more ammonia is produced in the reaction chamber, using up the nitrogen and hydrogen, the reaction will slow down and eventually stop. This would happen before all the nitrogen and hydrogen were used up: the presence of the ammonia slows the reaction. Extracting the ammonia product and pumping in more ingredients will keep production continuous.

This is an example where the engineering is driven by the chemistry. Without an understanding of how ammonia is made by this reaction, and how chemical reactions behave in practice, it would be an extremely inefficient process, and indeed perhaps impossible to manufacture ammonia on any viable industrial scale. Yet the chemical knowledge is insufficient without the engineering expertise to build a plant to the required specification: a plant that will fulfil the conditions that I have outlined above.

Having collected the arguments from chemistry on the conditions to make ammonia it remains to ask how to make it quickly. Typically plant will only be economic at production rates of a few thousand tonnes per day. The optimum pressures and temperatures need to be found. That is a job for theory and for development research.

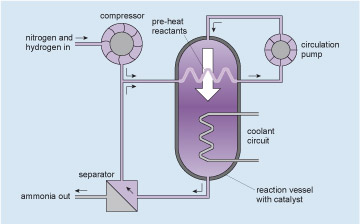
So, with all this science understood, our chemical engineers have to design and build a system that takes advantage of it. Figure 16 indicates the principles of the plant.

Maximise

Figure 16 Ammonia production

Show description|Hide description

Figure 16 is a schematic simplified layout or map of an ammonium production system which has 4 components connected by pipelines. The largest component is a reaction vessel with catalyst and this is located in the centre of the layout. It is shown in section form so that the internal details can be displayed. The top and bottom are sealed with semicircular ends. There is a vertical inlet at the top and a vertical outlet at the bottom. A horizontal but zigzagged pipeline crosses through the vessel which represents a heat exchanger that takes heat out of the gases in the reaction vessel and transfers it into the gases flowing through the pipe. Further down the vessel there is another zigzagged pipeline passing through the reaction vessel which represents another heat exchanger. This heat exchanger takes more heat out of the gases in the reaction vessel and transfers it into a coolant circuit. The details of the coolant circuit are not shown. A compressor is located in the top left-hand corner and is shown as a round object with internal rotating vanes. The vanes are curved to symbolise the ability to increase pressure. There is a horizontal pipe inlet on its left side and a vertical pipe outlet at the bottom. In the top right hand corner of the layout there is a circulation pump. The symbol for the pump is the similar to the compressor but it is smaller with straight vanes. The straight vanes indicate that this pump increases flow but not pressure. There is a vertical inlet pipe at the bottom and a vertical outlet pipe at the top. In the bottom left hand corner there is a separator unit. This is shown as a square with a diagonal line going from the top left corner to the bottom right corner. There is a horizontal inlet pipe on its right side, a vertical outlet pipe on the top and another horizontal outlet pipe on its left side. There are pipelines shown connecting these components. They are depicted using two parallel lines about 1 mm apart and they are either horizontal or vertical. An arrow next to the pipeline indicates the direction of flow which can be up or down, or to the right or to the left.

A horizontal pipeline enters the layout at the top left hand corner and carries nitrogen and hydrogen into the system, flowing to the right. It connects to the left inlet of the compressor. From the bottom outlet of the compressor, a vertical pipe flows down to meet a vertical pipe flowing up from the separator. At the meeting of these pipelines there is a T junction. Imagine the T is on its side with the normally vertical part of the T now horizontal flowing to the right. The two vertical pipelines flow into the T and then flow out of the T to the right. The pipeline continues to the right and connects with the left side inlet of the upper heat exchanger that is in the reaction vessel. Connected to the right side outlet of the heat exchanger is a horizontal pipeline which continues to flow to the right. It then turns left to become vertical and flows up to connect with the bottom inlet of the circulation pump. Connected to the outlet of the circulation pump is vertical pipeline which flows up. It then turns left to become horizontal and flows to the left. It then turns left again to become vertical and flows down. This pipeline then connects to the top inlet of the reaction vessel. Connected to the bottom outlet of the reaction vessel is a vertical pipeline which flows down. It then turns right to become horizontal and flows to the left. This pipeline then connects to the inlet on the right side of the separator unit. A vertical pipeline is connected to the top outlet of the separator unit and carries unreacted nitrogen and hydrogen which flows up to connect to the T junction mentioned before. A horizontal pipeline is connected to the other left outlet of the separator and flows to the left, carrying ammonia out of the system. The pipeline leaves the layout at the bottom left hand corner.

Figure 16 Ammonia production

The gases at high pressure are pumped around the circuit shown (follow the arrows starting at the circulation pump, which pumps the mixed, but unreacted, ingredients into the reaction vessel). The gases enter the reaction vessel at the top and some of the nitrogen and hydrogen react to form ammonia as they pass over a catalyst within the reaction vessel (see Catalysts and converters ). The mixture leaving the reaction vessel at the bottom passes to the separator where the ammonia product is removed. The unreacted nitrogen and hydrogen, together with enough extra nitrogen and hydrogen injected from the compressor to make up for what has reacted, return to the pump via a heat exchanger within the reaction vessel which both pre-heats the reactants and removes some of the reaction heat. More excess heat is removed from the reaction vessel by the coolant circuit. Thus a continuous production of ammonia is achieved. I will not go into the subtleties of the internal design of the reaction vessel which make the process efficient, nor of the control systems which link the heat and gas flows. Rather I will concentrate on the engineering of the reaction vessel itself.

The ammonia reaction vessel is large, perhaps a cylinder 20 m high by 2 m in diameter, which has a volume of about 63 m ³ (see Units of area and volume ). For efficient performance, the pressure needs to be about 350 times atmospheric pressure (or '350 atmospheres').

The contents of the reaction vessel, at a temperature of several hundred degrees Celsius, include a poisonous gas, ammonia, and an explosive one, hydrogen. The consequences of a leak could be extremely dangerous. So, beyond the primary engineering to provide function, an additional issue here is safety. How do you make a vessel of that size, capable of holding the pressure, with at least six pipes going into it, and guarantee that it is safe? The answer lies largely in 'past practice'. Because pressure vessels have been made for a long time, for many purposes (for example, high-pressure steam boilers in power stations), the 'know how' has gradually developed. Each increment of extra performance demanded from time to time has pushed knowledge a bit further, and the occasional accident serves as a salutary reminder that we don't always get it right.

Units of area and volume

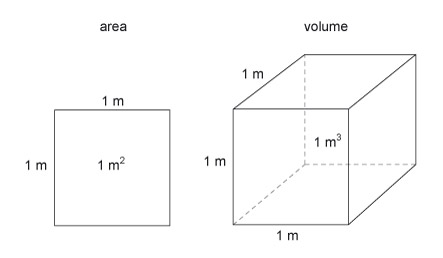
The basic units of area and volume are the 'square metre' (m ² ) and the 'cubic metre' (m ³ ) (Figure 17). These are simply shapes which have sides that are 1 m in length.

Figure 17 Units of area and volume

Show description|Hide description

Figure 17 consists of two diagrams; one represents a unit of area and the other represents a unit of volume. The unit of area is represented by a square. Each side is labelled as being 1 metre long and the space bounded by the square is labelled as being 1 metre squared. The unit of volume is represented by a cube. The cube is drawn using a technique of drawing called oblique projection. Whenever a cube is viewed, only 3 of the 6 faces will be visible and their shape will always be distorted by the effects of perspective. Perspective drawing is very difficult and time consuming and so engineers utilize other methods of drawing a solid object. Oblique projection is perhaps the easiest as one face of the object is drawn using its true geometric shape. In this case, one face of the cube is drawn as a square. The right hand surface and the top surface are also visible. Consider the top surface. The edge shared with the front surface is horizontal, and the edge shared with the rear hidden surface is also horizontal. The side edges are drawn at an angle which in this case is about 38 degrees. The sides are drawn a little shorter. The top surface is therefore drawn as a parallelogram. Consider the right hand side surface. The edge shared with the front surface is vertical, and the edge shared with the rear hidden surface is also vertical. The top edge is shared with the top surface and is at the same angle of about 38 degrees. The bottom edge is shared with the hidden bottom surface of the cube and is parallel with the top edge. The side surface is therefore drawn as a parallelogram. A cube has 12 edges but only 9 edges are visible. Although a square has 4 edges and three square surfaces are visible, the side and top surfaces each share an edge with the front surface and share another edge with each other. The cube has another 3 edges and 3 surfaces that are not visible to the viewer. The hidden edges are shown using another technique of drawing – they are drawn with dashed lines. One of these hidden edges is vertical, one is horizontal and the other is at the angle of about 38 degrees. A cube has 8 corners but only 7 are visible. The three hidden lines join at that hidden corner and as a result the three hidden surfaces are revealed by the geometry of the lines. Each side of the cube is labelled as 1 metre long and the space inside the cube, which represents the volume of the cube, is labelled as 1 metre cubed.

Figure 17 Units of area and volume

Square metres are inconveniently small for measuring land holdings so the French Revolutionary Committee decided to define 100 m ² (i.e. 10 m × 10 m) as 1 are (pronounced 'air'). A more frequently used measure of land area is the 'hectare'.

Activity 6 (example)

Use Table 1 in Section 1.2.1 to remind yourself what 'hect' means and then work out how many square metres there are in a hectare.

Answer

'Hect' means × 100, so 1 hectare is 100 are, which is

• 100 × 100 m ² = 10 000 m ².

Cubic metres, on the other hand, are inconveniently large for measuring a person's daily intake of food or drink. You will often come across the cubic centimetre, cm ³ (i.e. 1 cm × 1 cm × 1 cm, or 0.01 m × 0.01 m × 0.01 m) or other units derived from the metre. A related unit of volume, the litre, has also been defined and is commonly used to measure volumes of liquid. A litre is the volume of a cube of 1 decimetre – or 10 cm edge length. The symbol for 'litre' is its initial letter, l, but this is so easily confused with the number 1 (for example, eleven litres can be written as 11 l) that it is usually safest to write out the word litre.

An even smaller unit of volume, the millilitre, is also useful. It is one thousandth of a litre. The symbol for millilitre is ml, which is not as ambiguous as the litre symbol.

Activity 7 (self-assessment)

• a.Use Table 2 in Section 1.2.1 to remind yourself what 'deci' means, and then work out how many litres there are in a cubic metre.
• b.A bottle of water has a volume of 500 ml. How many cl is this?
• c.What is the relationship between 1 ml and 1 cm ³ ?
• d.The standard size of a British brick is 215 mm × 102.5 mm × 65 mm. First guess its volume in litres, then calculate it.
• e.How many bricks make a cubic metre of wall (ignoring the mortar)?

Answer

• a.The 'deci' prefix means × 1/10, which is equivalent to ÷10, so there are 10 dm in one metre. Hence,
  • 1 m ³ = 10 × 10 × 10 dm ³ = 1000 litres.
• b.The 'milli' prefix means ÷1000. The 'centi' prefix means ÷100. So there are 10 ml in 1 cl and, therefore, 500 ml = 50 cl.
• c.10 cm = 1 dm so
  • 10 × 10 × 10 cm ³ = 1 dm ³ = 1 litre.
  • So 1000 cm ³ make 1 litre, and hence 1 ml is the same as 1 cm ³.
• d.The dimensions of the brick in cm are 21.5 cm × 10.25 cm × 6.5 cm.
  • The volume of the brick in cm ³ is therefore
  • 21.5 × 10.25 × 6.5 cm ³ 1432 cm ³.
  • But 1 ml is the same as 1 cm ³ so the volume of the brick is 1432 ml, or 1.432 litres.
  • My guess, thinking of a litre box of drink by comparison, was that the brick was 'similar' and would have a volume of about one litre. I was wrong by a factor of 1.432.
• e.There are 1000 litres in a cubic metre. We know from (d) that each brick is 1.432 litres in volume, so we'll need 1000/1.432 = 698.3 bricks; in other words, approximately 700 bricks.