2 Examples of surfaces
2.1 Surfaces in space
In Section 2 we start by introducing surfaces informally, considering several familiar examples such as the sphere, cube and Möbius band. We also illustrate how surfaces can be constructed from a polygon by identifying edges. A more formal approach to surfaces is presented at the end of the section.
Figure 3 shows some simple examples of surfaces in three-dimensional space.
Since we are interested only in the surface of such objects, rather than the interior, you should always think of such objects as being hollow, rather than solid. Such surfaces, being subsets of ![]() 3, are given the subspace topology from
3, are given the subspace topology from ![]() 3.
3.
In each of the examples in Figure 3, the surface is locally like part of the plane, as illustrated in Figure 4. This means that, for each point x of the surface, we can find a subset of the surface that contains x and is homeomorphic to an open disc in the plane: we call such a subset a disc-like neighbourhood of x. (A neighbourhood of a point x is an open set containing x.) Such a neighbourhood is an open subset of the surface in the subspace topology that it inherits from ![]() 3.
3.
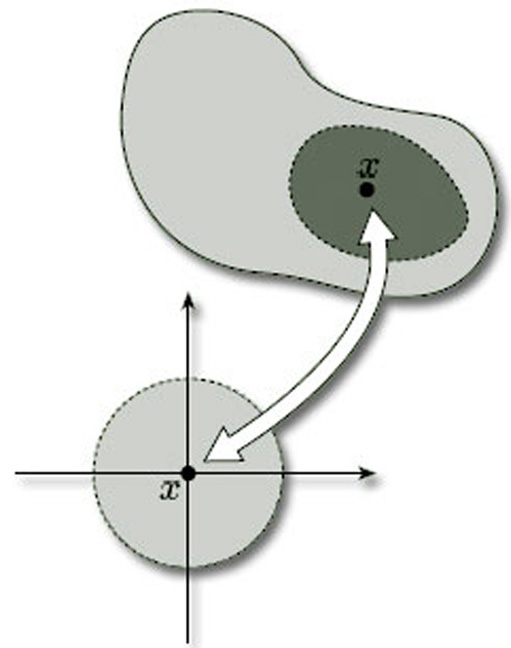
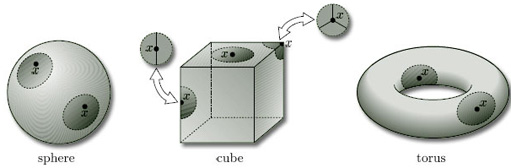
Figure 5 shows some disc-like neighbourhoods in three of the surfaces of Figure 3. Notice that a disc-like neighbourhood may be curved or bent in space, or may even have folds in it.
Problem 1
Draw some disc-like neighbourhoods on a 2-fold torus.
Answer

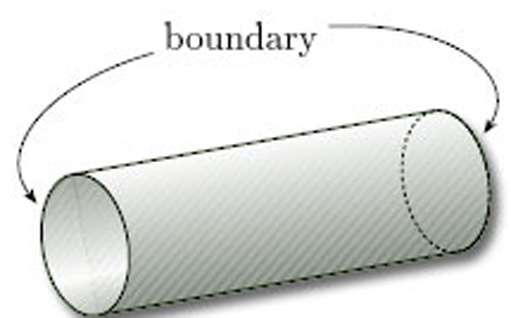
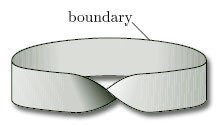
All the objects we wish to consider as surfaces have many points with disc-like neighbourhoods. However, there are some surfaces where some of the points do not have such neighbourhoods. Two common examples are shown in Figure 6 – a hollow cylinder, open at both ends, and a Möbius band.

Two neighbourhoods of points on the cylinder are shown in Figure 7. These illustrate that, except for the points at the ends of the cylinder, each point has a disc-like neighbourhood; but the points at the ends have no such neighbourhoods. Instead, each such endpoint x has a half-disc-like neighbourhood – a subset that is homeomorphic to an open half-disc in the upper half-plane, considered as a subspace of ![]() 2, as shown in Figure 8. Such a neighbourhood is again an open subset of the surface in the subset topology that it inherits from
2, as shown in Figure 8. Such a neighbourhood is again an open subset of the surface in the subset topology that it inherits from ![]() 3.
3.

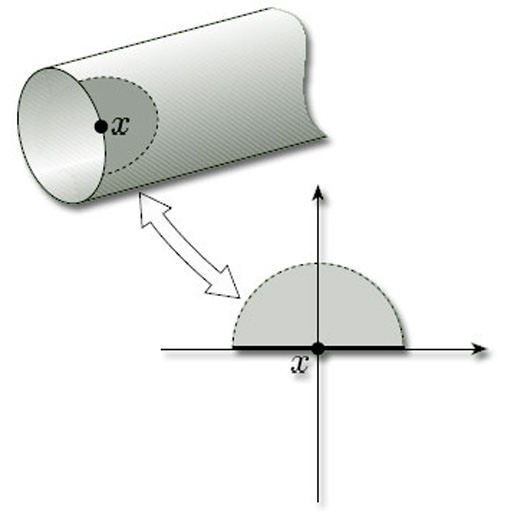
The upper half-plane includes the points on the horizontal axis. The open half-discs are those with diameter along that axis and include the axis points; they are open subsets of the closed half-plane in the subspace topology inherited from ![]() 2.
2.
Problem 2
Draw some disc-like and half-disc-like neighbourhoods on a Möbius band.
Answer

In fact, all the objects we wish to consider have surfaces that are characterised as consisting of points that have either disc-like or half-disc-like neighbourhoods. This leads to the following provisional definition.
Provisional definition
A surface is a topological space (X, T) with the property that each point of X has a neighbourhood that is homeomorphic either to an open disc in the plane or to an open half-disc in the upper half-plane, i.e. given any point x ![]() X, there is an open set U containing x such that U is homeomorphic either to an open disc in
X, there is an open set U containing x such that U is homeomorphic either to an open disc in ![]() 2 or to an open half-disc in the upper half-plane with the subspace topology inherited from the Euclidean topology on
2 or to an open half-disc in the upper half-plane with the subspace topology inherited from the Euclidean topology on ![]() 2. The open set U is called a disc-like neighbourhood, or half-disc-like neighbourhood of x, as the case may be.
2. The open set U is called a disc-like neighbourhood, or half-disc-like neighbourhood of x, as the case may be.
(We shall modify this definition slightly at the end of this section.)
This idea of points of a surface having disc-like neighbourhoods or half-disc-like neighbourhoods is crucial to the concept of a surface. In the following worked problem we present an object that looks as though it might be a surface, but fails to be so because it has a point with no such neighbourhood.
Worked problem 1

Explain why the double cone, open at both ends, is not a surface.
Solution
Although most points on the double cone have disc-like or half-disc-like neighbourhoods, the point z in the middle, indicated in Figure 10(a), does not. One way to see this is to note that if we remove the point z, then the neighbourhood breaks into two pieces, as shown in Figure 10(b). This cannot be the case if the neighbourhood is homeomorphic to a disc or half-disc: removing a single point from a disc or half-disc cannot split it into two pieces.
Since we have found a point with no disc-like or half-disc-like neighbourhood, the double cone is not a surface.
Problem 3
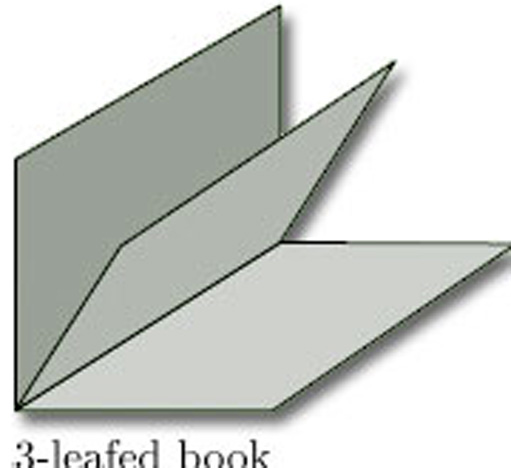
Explain why the 3-leafed book, illustrated in Figure 11, is not a surface.
Answer
No point on the spine of a 3-leafed book has a disc-like or half-disc-like neighbourhood. If we remove the spine, then the neighbourhood of any point on the spine breaks into three pieces, as shown. This cannot be the case if the neighbourhood is homeomorphic to a disc or half-disc.
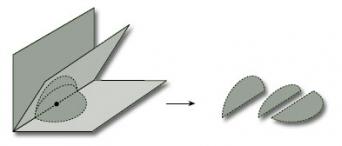
Since no point on the spine has a disc-like or half-disc-like neighbourhood, the 3-leafed book is not a surface.
The points of a surface with half-disc-like neighbourhoods, such as the endpoints of a cylinder, can be thought of as lying on the boundary of the surface.
Definitions
Let S = (X, T) be a surface.
A boundary point of S is a point of X for which every neighbourhood contains a half-disc-like neighbourhood.
The boundary of S is the set of all boundary points of S.
A surface with boundary is a surface whose boundary is non-empty.
A surface without boundary is a surface with no boundary points.
An example of a surface with boundary is a cylinder, whose boundary consists of the two circular ends (Figure 12). An example of a surface without boundary is a sphere, since each point has a disc-like neighbourhood (Figure 5).
Problem 4
Identify the boundary of each of the following surfaces:
(a) a Möbius band;
(b) a torus.
Answer
(a) The boundary consists of the single edge.
(b) Since each point has a disc-like neighbourhood, there is no boundary, i.e. the boundary is the empty set.
The following theorem describes the boundary of a surface.
Theorem 1
The boundary of a surface is composed of a finite number of arcs, each of which is homeomorphic to a circle or to a unit interval, or it is the empty set.
(We omit the proof, which is beyond the scope of this course.)
Up to now our surfaces have been ones that can be embedded in three-dimensional space. We give these a special name.
Provisional definition
A surface in space is a surface (X, TX) where X is a subset of ![]() 3 and TX is the subspace topology on X inherited from the Euclidean topology T on
3 and TX is the subspace topology on X inherited from the Euclidean topology T on ![]() 3.
3.
Since our definition of a surface is provisional, this definition of a surface in space is provisional also.
In Section 2.3 we shall meet some surfaces that cannot be embedded in three-dimensional space.


