4.6.1 Remarks
-
We already know that the characteristic numbers are topological invariants, that is, any two homeomorphic surfaces have the same values for the characteristic numbers. Thus it is solely the converse, namely if two surfaces have the same values for the characteristic numbers then they are homeomorphic, that we have to prove.
It follows from the Classification Theorem that if we restrict our attention to orientable surfaces (ω = 0), then the numbers β and χ characterise the surface completely – and similarly if we restrict our attention to non-orientable surfaces (ω = 1).
Our assumption that all surfaces are compact guarantees that the characteristic numbers are finite,
-
The Classification Theorem allows us to refer to the sphere, the torus, the Klein bottle, etc., rather than a sphere, a torus and a Klein bottle, etc.
Problem 24
Which surfaces are characterised by the following sets of characteristic numbers?
Answer
-
Sphere.
-
Möbius band.
-
Torus with 1 hole.
-
2-fold torus.
-
Projective plane.
Problem 25
Find the characteristic numbers of the surface obtained by gluing two Möbius bands along their boundaries. Deduce from the Classification Theorem that this surface is homeomorphic to the Klein bottle.
Answer
The surface obtained by gluing two Möbius bands together has no boundary components (β = 0), and is non-orientable (ω = 1). Also, by Theorem 13, its Euler characteristic is the sum of the Euler characteristics of each separate surface, so χ = 0 + 0 = 0. The Klein bottle has these values for its characteristic numbers, so (by the Classification Theorem) the glued surface is homeomorphic to the Klein bottle.
Worked problem 4
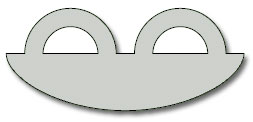
Find the characteristic numbers of the closed disc with two straps, shown in Figure 97.
Solution
The surface has three boundary components, so β = 3. The surface contains no Möbius band, and is therefore orientable, so ω = 0. To find the Euler characteristic, we choose a subdivision. The one shown in Figure 98 has 8 vertices, 12 edges and 3 faces, so χ = 8 − 12 + 3 = −1.
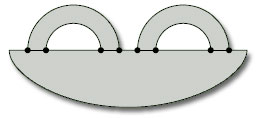
You could also argue that, as the surface is a closed disc with two holes, its Euler characteristic is 1 − 2= −1 (by Theorem 11).
Problem 26
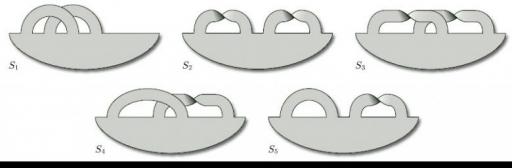
Consider the closed disc with two straps added in other ways, sometimes with a twist, as shown in Figure 99. Compute the characteristic numbers of each surface, and then use the Classification Theorem to determine which of these surfaces are homeomorphic.
Answer
Each surface has a subdivision with 8 vertices, 12 edges and 3 faces, as indicated in Worked Problem 4. The Euler characteristic of each surface is therefore −1, as before.
The characteristic numbers β and ω are as follows.
| surface | S1 | S2 | S3 | S4 | S5 |
| β | 1 | 1 | 2 | 1 | 2 |
| ω | 0 | 1 | 1 | 1 | 1 |
It follows from the Classification Theorem that the surfaces S2 and S4 are homeomorphic, as are the surfaces S3 and S5; no other two surfaces are homeomorphic.
Problem 27
For each of the following paper surfaces, mark a subdivision and hence determine the characteristic numbers of the surface.
Answer
(a) We have drawn a subdivision with 12 vertices.
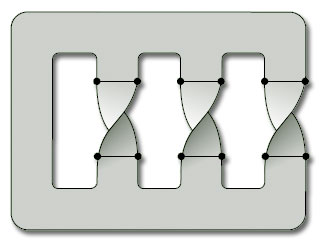
There are 18 edges and 4 faces, so the Euler characteristic is χ = 12 − 18 + 4 = −2.
There is one boundary component, so β = 1.
The surface is non-orientable (see Worked Problem 2(b)), so ω = 1.
(b) We have drawn a subdivision with 16 vertices.
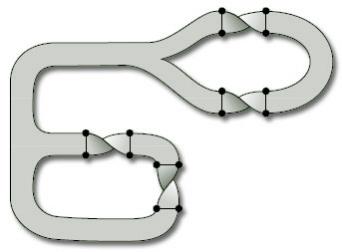
There are 24 edges and 7 faces, so the Euler characteristic is χ = 16 − 24 + 7= −1.
There are three boundary components, so β = 3.
The surface is orientable (see Solution 14(b)), so ω = 0.
For future reference, we conclude this section with a table of some common surfaces with their characteristic numbers.
| surface | β | ω | χ |
|---|---|---|---|
| sphere | 0 | 0 | 2 |
| n-fold torus | 0 | 0 | 2 − 2n |
| Klein bottle | 0 | 1 | 0 |
| projective plane | 0 | 1 | 1 |
| closed disc | 1 | 0 | 1 |
| cylinder | 2 | 0 | 0 |
| Möbius band | 1 | 1 | 0 |
In addition, adding a hole to any surface increases its boundary number β by 1, keeps its orientability number ω the same, and decreases its Euler characteristic χ by 1.