1 Topological spaces and homeomorphism
Two topological spaces (X, TX) and (Y, TY) are homeomorphic if there is a bijection f : X → Y that is continuous, and whose inverse f−1 is also continuous, with respect to the given topologies; such a function f is called a homeomorphism. The relation ‘is homeomorphic to’ between topological spaces is the most fundamental relation in topology, because two topological spaces that are homeomorphic are indistinguishable from a topological point of view – they are topologically equivalent. An alternative definition of a homeomorphism is that a bijection f : X → Y is a homeomorphism if and only if both f and f−1 map open sets to open sets. Thus, if (X, TX) and (Y, TY) are homeomorphic, then not only are the elements of X and Y in one–one correspondence, but so also are their open sets. We can thus regard (Y, TY) as being essentially the same space as (X, TX), so far as its purely topological properties are concerned: (X, TX) and (Y, TY) are merely two different ways of presenting the same space.
It is therefore useful to be able to determine whether two given topological spaces are homeomorphic. Of course, if we can find a specific homeomorphism between them then the question is answered; but if we fail to find a homeomorphism then we cannot deduce that there isn't one. So looking for a particular homeomorphism may not be the best approach. What we want are criteria that enable us to tell whether two given surfaces are homeomorphic without our having to try to construct a specific homeomorphism between them.
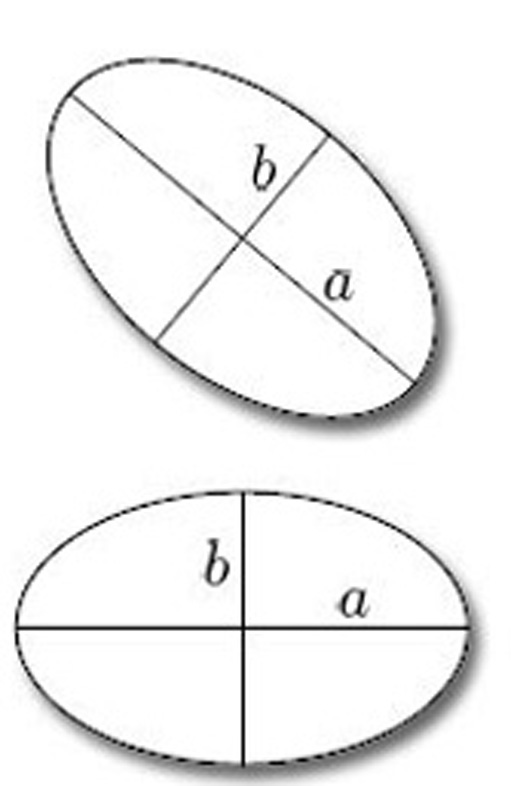
A similar situation, which may help to clarify what is involved, is the following. A map between metric spaces that preserves distances is called an isometry, and two subsets of a metric space that are related by an isometry are essentially the same, so far as their metrical properties are concerned. For example, consider the collection of ellipses in ![]() 2, with the Euclidean metric. Two ellipses are isometric if and only if the lengths of their major axes are the same, and the lengths of their minor axes are the same (see Figure 1). These two criteria enable us to determine whether two given ellipses are isometric without our having to construct a specific isometry between them: we simply compare the lengths of their axes. We say that the lengths of the major and minor axes classify ellipses in
2, with the Euclidean metric. Two ellipses are isometric if and only if the lengths of their major axes are the same, and the lengths of their minor axes are the same (see Figure 1). These two criteria enable us to determine whether two given ellipses are isometric without our having to construct a specific isometry between them: we simply compare the lengths of their axes. We say that the lengths of the major and minor axes classify ellipses in ![]() 2 up to isometry.
2 up to isometry.
Notice that, in the phrase ‘classify ellipses in ![]() 2 up to isometry’, we have specified the class of figures under consideration (ellipses in
2 up to isometry’, we have specified the class of figures under consideration (ellipses in ![]() 2): our criteria apply only to these particular figures in the plane, and we make no claim that other figures can be classified up to isometry in a similar way. Note also the importance of including the qualification ‘up to isometry’, since all ellipses are homeomorphic.
2): our criteria apply only to these particular figures in the plane, and we make no claim that other figures can be classified up to isometry in a similar way. Note also the importance of including the qualification ‘up to isometry’, since all ellipses are homeomorphic.
In this course, our main task is to define a certain class of surfaces called compact surfaces, and then to specify criteria that allow us to determine whether two given compact surfaces are homeomorphic. These surfaces can be classified using just three criteria, as we shall show. Indeed, just as we can classify ellipses in ![]() 2 up to isometry by specifying just two numbers (the lengths of the major and minor axes), so we can classify all compact surfaces up to homeomorphism by specifying just three numbers. The appropriate theorem – the Classification Theorem – is stated later in this course. Before we state the Classification Theorem, we give examples of surfaces, show how they can be manipulated, defined and represented, and examine some of their important properties.
2 up to isometry by specifying just two numbers (the lengths of the major and minor axes), so we can classify all compact surfaces up to homeomorphism by specifying just three numbers. The appropriate theorem – the Classification Theorem – is stated later in this course. Before we state the Classification Theorem, we give examples of surfaces, show how they can be manipulated, defined and represented, and examine some of their important properties.
The spirit in which we explore surfaces in this course arises from the way that the theory of surfaces relates to the rest of topology, and that in turn is reflected in the history of these subjects. When studying surfaces we can proceed a long way with intuitive concepts, and the subject is often studied in that fashion. Today we may appeal to these intuitions, secure in the knowledge that the intuitively appealing theorems can be proved rigorously. Indeed, the precise definitions and rigorous proofs appearing in the literature frequently involve subtle and difficult arguments of a kind otherwise out of keeping with geometric topology, and may add little to our understanding of the underlying concepts.
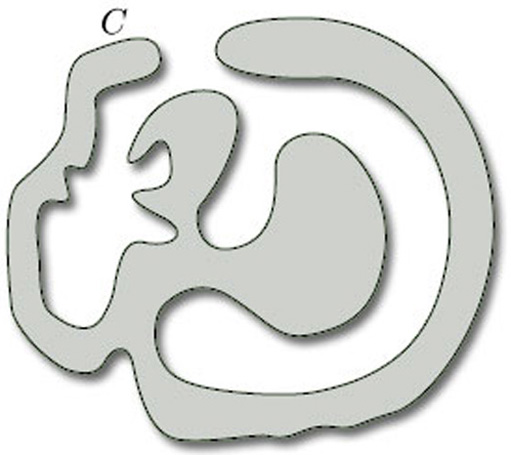
An example is the so-called Jordan Curve Theorem, which asserts that any curve in the plane that is homeomorphic to a circle divides the plane into two regions, one bounded (the ‘inside’ of the curve) and the other unbounded (the ‘outside’); Figure 2 shows such a curve C in the plane, with its inside shaded. Although the statement of the Jordan Curve Theorem is entirely plausible – indeed, it is fundamental to many parts of mathematics – the theorem is difficult to prove. In fact, it is likely that few mathematicians have ever seen a proof, because such proofs merely confirm what we already believe. It is good to have a proof, of course, but we do not consider it essential to prove all of the results in this course. Examining the proof of the Jordan Curve Theorem reveals no particularly counter-intuitive complications, and so we omit the proof.
In this course we indicate when concepts are to be understood at an intuitive level, and when more precise definitions, theorems and proofs are required. Where possible, we provide rigorous definitions and proofs.
