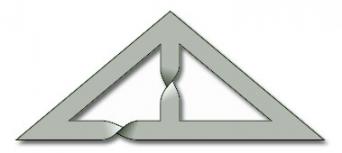
3.1.1 Inserting half-twists
We can insert half-twists into a paper surface whenever a piece of the surface is homeomorphic to a rectangle ABCD with the following properties:
the edges AB and CD of the rectangle map to distinct parts of the boundary of the surface, and the edges BC and DA of the rectangle map to non-boundary points of the surface.
As illustrated in Figure 51, the process of inserting a half-twist consists of cutting out the rectangle, giving it a half-twist so that the edge DA appears as it was but the edge BC is in the opposite direction, and then gluing it back.

Since inserting a half-twist is not a homeomorphism, this process allows us to create new surfaces.
As well as creating a new surface, inserting a half-twist can change the boundary number. For example, Figure 52(a) shows a paper surface with boundary number β = 3. If we give the marked rectangle a half-twist, as shown on the right, then we obtain a surface with boundary number β = 2.
Problem 12
Starting with the paper surface shown in Figure 52(b), insert a half-twist to produce a surface with boundary number β = 1.
Answer
One way to insert a half-twist to obtain a surface with boundary number β = 1 is the following: