2.4.1 Remarks
-
This theorem applies to all surfaces and not just to surfaces in space.
-
This theorem tells us that the boundary number is a topological invariant for surfaces, i.e. a property that is invariant under homeomorphisms.
-
It follows from the theorem that two surfaces with different boundary numbers cannot be homeomorphic. It does not follow that two surfaces with the same boundary number are homeomorphic – for example, a sphere and a torus both have boundary number 0, but are not homeomorphic (as we demonstrate below).
-
Another consequence of the theorem is that a surface with non-zero boundary number cannot be homeomorphic to a surface with boundary number 0 – that is:a surface with boundary cannot be homeomorphic to a surface without boundary.
This seems reasonable, because such a homeomorphism would have to take the half-disc-like neighbourhoods of a boundary point to disc-like neighbourhoods of the image point.
Problem 10
Use boundary numbers to show that a Möbius band and a 2-fold torus are not homeomorphic.
Answer
For the Möbius band, β = 1; for the 2-fold torus, β = 0. Since these numbers are different, the surfaces are not homeomorphic, by Theorem 2.
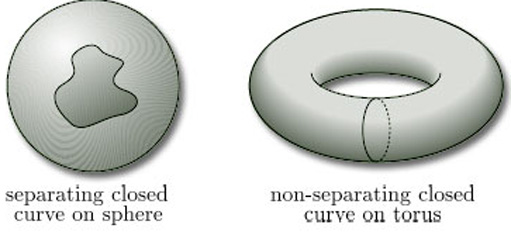
For surfaces in space with the same boundary number, there is another practical test that can sometimes be used to confirm that they are not homeomorphic. It requires the consideration of closed curves on the surface. For example, consider a sphere and a torus, both of which have boundary number 0. Observe that any closed curve on the sphere that does not cross itself separates the sphere into two regions, whereas there are closed curves on the torus that do not (see Figure 44). If the sphere and the torus were homeomorphic, then a non-separating curve on the torus would map by the homeomorphism onto a non-separating curve on the sphere, which is not possible. (This is the Jordan Curve Theorem mentioned in Section 1.)