2.3.7 Two-fold torus
As the polygons become more complicated, so the identifications become more difficult to visualise. For example, what happens if we try to identify the edges of an octagon in pairs, as indicated by the edge labels and arrowheads in Figure 34? Figure 35 shows that identifying, in the directions indicated, the edges labelled a and the edges labelled c results, after some bending and stretching, in a cylinder bounded by edges labelled b and d. If we now identify, in the directions indicated, the edges labelled b and the edges labelled d, we obtain, after some bending and stretching, a 2-fold torus. One way of seeing this is first to pull together the edges labelled a and c in the holed cylinder, creating two holes bounded by edges b and d, and then to bend round the cylinder ends to meet these holes.
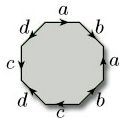
In a similar way, one could obtain a 3-fold torus by identifying the twelve edges of a dodecagon in pairs, and in general an n-fold torus from a 4n-sided polygon, for all natural numbers n.

