5.6.2 Structure and crystallinity
In addition to the structural constraints mentioned in Section 2, where tacticity and geometrical isomerism control whether or not a polymer chain can crystallise, molecular mass and copolymerization are other important variables which can influence crystallising properties. A related effect is plasticization where a low molecular mass material is deliberately added to lower Tg or Tm.
The lowering of melting point caused by copolymerization will generally affect Tg in a similar way. It can be shown from classical thermodynamics that the melting point of a crystalline homopolymer (Tm°) will be lowered to a value Tm (in K) by the presence of x mole fraction of randomly copolymerized repeat units (B) according to the equation
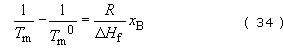
where R is the gas constant and ΔH f the heat of fusion per mole of homopolymer repeat unit. The equation predicts that the melting point depression is directly proportional to the mole fraction of the second component (B) and inversely proportional to the heat of fusion.
Since chain ends can also be regarded as ‘impurities’ in a chain which will lower the melting point, a similar equation can be derived for the effect of molecular mass:
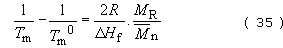
Since most polymers show less than 100 per cent crystallinity, observable heats of fusion will be proportionally lower depending on the exact degree of crystallisation. However, the melting points are unaffected by the presence of amorphous material. A further quantity of interest for crystalline polymers is the entropy of fusion, ΔS f. It is simply related to T m0 by the equation
Self assessment question 11
(a) At what number-average molecular mass will the melting point of polypropylene be 99.9 per cent of that for very high molecular mass polymer?
(b) In material of molecular mass such that chain ends are not important, what is the effect on the crystalline melting temperature Tm of randomly copolymerizing 10 mole% ethylene into the homopolymer? What would be the practical consequences in terms of processing the copolymer to shape and the service properties of the copolymer?
Answer
(a) The effect of molecular mass on the melting point is readily evaluated from Equation (35):
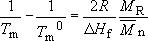
i.e.
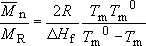
If Tm = 0.9997Tm0, then
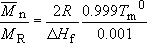
The following are values for polypropylene :
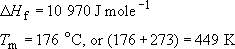
So using these values in the above equation, together with a value for R = 8.314 J K−1 mole−1
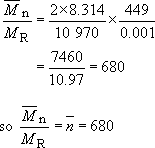
The molecular mass of the polypropylene repeat unit is
(3 × 12) + (6 × 1) = 42, so the number average molecular mass of PP will be 42 × 680 or 28600. The melting point at this value of 
is about 448.5 K, about half a degree less than the value for very high molecular mass material.
(b) The effect of randomly copolymerizing 10 per cent; ethylene can be found from Equation (34)
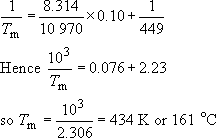
The net result is that the melting point is depressed by 15 °C, which means that processing to shape will be less energy consuming. On the other hand, the upper limit on service temperature will also be reduced compared to the homopolymer. The lower limit, which is related to Tg rather than Tm will be depressed below 0 °C – a big advantage for low temperature usage. Milk crates or other containers exposed to UK outside temperatures would be better constructed from copolymer rather than homopolymer. The depressant effect for partial block copolymers will not be dissimilar to that produced in random copolymerization. The degree of crystallinity will also be depressed owing to the disruption of the crystalline lattice by the copolymer blocks. This will reduce the stiffness of the material.