3 बीजगणितीय सर्वसमिकाओं को गुणन की विशेष स्थितियों के रूप में देखा जाता है
विद्यार्थी बीजगणितीय सर्वसमिकाओं को अक्सर कोई जादू या यथार्थ सत्य समझ लेते हैं। शायद ही उन्हें इस बात का बोध होता है कि ये सर्वसमिकाएँ कहाँ से आती हैं या यह कि वे गुणन की विशेष परिस्थितियाँ हैं।
सर्वसमिकाओं को याद करने की विद्यार्थियों की आदत का एक कारण यह है कि वे सर्वसमिका द्वारा चित्रित संबंध के साथ कोई तादाम्य स्थापित करने में विफल रहते हैं। आपने ध्यान दिया होगा कि विद्यार्थी निम्न प्रकार के सर्वसमिकाओं को वापस याद करते समय सामान्य त्रुटियाँ करते हैं:
भले ही यह देखना बहुत ही सरल है कि क्या दो कथन सही हैं (बस उन्हें चरों के कुछ मानों को सत्यापित करना होता है), विद्यार्थी ये गलतियाँ करना जारी रखते हैं। कभी–कभी विद्यार्थी इस बात से अंजान रहते हैं कि वे अपने कथनों को कितनी आसानी से सत्यापित कर सकते हैं। एक अन्य और अधिक गंभीर कारण यह है कि उन्होंने कभी भी इन कथनों के भौतिक (या ज्यामितीय) अर्थ को नहीं समझा।
इन सर्वसमिकाओं को समझने में अपने विद्यार्थियों की मदद करने के लिए आप पिछले अनुभाग में बताई गई मानसिक चित्रण तकनीकों का उपयोग कर सकते हैं। गतिविधि 2 आपको अपने विद्यार्थियों की भिन्न–भिन्न सर्वसमिकाओं का मतलब स्वयं पता करने में मदद करने की विधि बताती है। यह काम बीजगणितीय सर्वसमिकाओं के प्रतिमानों का पता लगाने, देखने और सामान्यीकृत करने पर केंद्रित है। अपनी समझ विकसित करने में मदद पाने के विचारों के बारे में बात करते समय विद्यार्थी किसी भागीदार के साथ काम करते हैं।
यह गतिविधि शुरू करने से पहले, यह पता कर लेना अच्छा होगा कि क्या आपके विद्यार्थी x + y और x − y की लंबाइयों को सही रूप में चित्रित कर लेते हैं। पहले वाले को समझना आसान है जबकि दूसरे वाले में थोड़ी अधिक मेहनत लगती है।
लंबाई ‘x + y’ का चित्रण
यदि सफेद भाग x है, और भूरा भाग y है, तो काला भाग x + y है। इसे ’भूरा’ भाग (x को दिखाने वाला) की लंबाई में सफेद भाग (y को दिखाने वाला) की जोड़ी गई लंबाई वही है जो काले भाग (x + y को दिखाने वाला) की है’ (चित्र 6 देखें)।
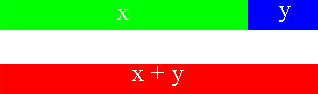
‘x – y’ की लंबाई को दिखाना
यदि सफेद भाग x है और भूरा भाग y है, तो काला भाग x − y है। इसे इस रूप में भी बताया जा सकता है कि ’सफेद भाग (x को दिखाने वाला) की लंबाई में से भूरा भाग (y को दिखाने वाला) को निकालने पर काला भाग (x − y को दिखाने वाला) बचता है’ (चित्र 7 देखें)।

गतिविधि 2: बीजगणितीय गुणनों की विशेष स्थितियों के रूप में बीजगणितीय सर्वसमिका
अपने विद्यार्थियों को निम्न बताएँ:
- अपने पड़ोसी को किसी गुणन तालिका के रूप में निम्न गणितीय व्यंजक बताएँ (आरेखित न करें या करके न बताएँ)। यह कैसा दिखाई देगा?
- a.(x + y)2
- b.(x + a)(x + b)
- c.(x − y)2
- d.(x − y)(x + y)
- अब हर व्यंजक का एक गुणन तालिका के रूप में निरूपण बनाएँ, जैसा कि आपने चरण 1 में बताया है।
- आपके द्वारा चरण 2 में बनाए गए क्षेत्रों को दिखाने वाले गणितीय व्यंजक को किसी भिन्न तरीके से लिखने का प्रयास करें।
- निम्न चार व्यंजकों में से हर एक के लिए चरण 1, 2 और 3 के अपने उत्तरों का अवलोकन करें और उनकी तुलना करें:
- चरण 3 में आपको व्यंजक (a), (b), (c) और (d) के लिए कितने पद मिले?
- ये पद किस तरह बने हैं?
- इन व्यंजकों में क्या समानता है? क्या अलग है? पदों के संगत क्षेत्र बॉक्स में रंग भरना मददगार हो सकता है।
- इस तरह से बीजगणितीय सर्वसमिका निकालने के नियम या विधि की व्याख्या करें, ताकि अन्य कक्षाओं के अन्य विद्यार्थी इस बारे में पढ़ सकें।
केस स्टडी 2: गतिविधि 2 के उपयोग का अनुभव श्रीमती कपूर बताती हैं
चूँकि मुझे लगता था कि कुछ विद्यार्थी ऐसे होंगे, जिन्हें संख्या से बीजगणित पर जाने में परेशानी होगी, इसलिए हमने पहले प्रश्न, (x + y)2, को एक पूरी कक्षा की गतिविधि के रूप में किया। इस कारण, और गतिविधि 1 में विद्यार्थियों द्वारा पहले ही गुणन तालिकाएँ बना लिए जाने के कारण, विद्यार्थी चरण 1 और 2 को काफी आसानी से कर पाए।
चरण 3 के कारण समतुल्यता के महत्व के बारे में एक चर्चा हुई। संकलित पदों वाला कोई व्यंजक उस व्यंजक के बराबर हो सकता है, जहाँ पदों को अभी तक संकलित नहीं किया गया है – यह केवल थोड़ा अधिक उलझनभरा दिखाई ही देता है। मैंने उनसे पूछा कि क्या वे इसे और भी अधिक उलझनभरा दिखाने के लिए कोई विचार दे सकते हैं, तो उनके पास कई विचार थे! इस पर हम सभी को हँसी आई, जो बहुत अच्छी बात थी, विशेष रूप से उन विद्यार्थियों के लिए, जो सामान्य तौर पर चुपचाप रहते हैं और जिनके मन में गणित को लेकर कुछ उत्सुकता होती है, वे भी मुस्कुराएँ और अधिक सहज दिखाई दिए।
चरण 4 का अंतिम भाग कठिन साबित हुआ। कठिनाई इसे समझाने में नहीं थी, बल्कि ऐसा संक्षेप में करने में थी। जिन वर्णनों के साथ हमने समापन किया वे बिल्कुल सही नहीं थे, लेकिन विद्यार्थी और मैं उनसे खुश थे। हम सबने महसूस किया कि बेहतर बनने के लिए हमें स्वयं के वर्णन और विधियाँ लिखने का और अभ्यास करने की आवश्यकता है।
हमने (a + b + c)2 को शामिल करने के लिए प्रश्नों का विस्तार किया और पदों को विभिन्न चिह्न देकर प्रयास किया, और उन्हें आसानी से समाधान प्राप्त हो गए।
हमने यह भी तय किया कि (a + b)3 या (a − b)3 करने के लिए हम इसे दो भागों में कर सकते हैं, (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2), और फिर इसे गुणन तालिका में रख सकते हैं।
विद्यार्थियों को बहुत खुशी हुई और उनमें इस तरह से काम करने का आत्मविश्वास जागा। एक विद्यार्थी ने कहा कि वह इतना चिंतामुक्त हो गया है कि वह अब अपनी याददाश्त विफल हो जाने पर बीजगणितीय सर्वसमिका को हल करके पता कर लेगा।
विचार के लिए रुकें पाठ के बाद विचार करने के लिए कुछ अच्छे प्रश्न हैं:
|
2 बीजगणितीय सर्वसमिकाओं की समझ विकसित करने के लिए मानसिक चित्रण
