3 गणितीय गुणधर्मों और तथ्यों को जानना
श्रीमती कपूर की कक्षा के विद्यार्थी इस बात के कुछ उदाहरण लेकर आए कि वे कोई गणितीय प्रमाण कैसे तैयार कर सकते हैं। हालाँकि, इनमें से किसी को भी गणितीय प्रमाण नहीं माना जा सकता, क्योंकि उपयोग किए गए तर्क पूरी तरह से स्वीकृत या स्थापित कथन नहीं थे। यद्यपि दूसरे सुझाव में इस तथ्य का उपयोग किया गया था कि किसी रेखा के कोणों का योग 180° होता है, लेकिन यह ’प्रमाण’ नहीं है कि तीन कोण हमेशा ’फिट’ होंगे। विद्यार्थी यह तर्क–वितर्क कर सकते हैं कि यह ’काम’ करेगा ही, लेकिन ऐसा औचित्य अनुभवसिद्ध साक्ष्य पर आधारित है, न कि किसी त्रिभुज के कोणों के गणितीय गुणधर्मों पर। प्रमेयों को सिद्ध करने का काम मौजूदा प्रमेयों और अभिगृहीतों के आधार पर किया जा सकता है; हालाँकि उन्हें आधार बनाकर कुछ करने से पहले आपको इनमें से कुछ बातें जाननी होंगी! जब आप कुछ को जान लेंगे, तो आप इनमें से अन्य कई का निगमन कर सकते हैं और अपनी स्वयं की उपप्रमेय बना सकते हैं।
गतिविधि 1 में कुछ ऐसे स्थापित और स्वीकृत कथन दिए गए हैं, जो विद्यालय के गणित में उपयोगी होते हैं। कुछ शास्त्रीय ज्यामिति से लिए गए हैं और उपरोक्त प्रमाण में उपयोगी हैं, लेकिन उदाहरण यह भी स्पष्ट करते हैं कि प्रमेयों का उपयोग ज्यामिति के अलावा कई अन्य क्षेत्रों में भी होता है। सूची में और चीज़ें जोड़ना, तथा दिए गए कथनों से अपने स्वयं के कुछ कथन निकालकर लिखने के लिए अपनी कल्पनाशीलता और प्राकृतिक निगमन कला का उपयोग करना विद्यार्थियों का काम है। ऐसी सोच को उकसाने के लिए यह वाक्य बहुत अच्छा हैः ’जब मुझे कुछ पता चलता है, तो मुझे कुछ और भी पता चलता है।’ ऐसा करके, विद्यार्थी विभिन्न अवधारणाओं के बीच संबंध भी स्थापित करेंगे और निगमन के अपने कौशल का अभ्यास करना शुरू करेंगे।
इस यूनिट में अपने विद्यार्थियों के साथ गतिविधियों के उपयोग का प्रयास करने के पहले अच्छा होगा कि आप सभी गतिविधियों को पूरी तरह (या आंशिक रूप से) स्वयं करके देखें। यह और भी बेहतर होगा यदि आप इसका प्रयास अपने किसी सहयोगी के साथ करें, क्योंकि जब आप अनुभव पर विचार करेंगे तो आपको मदद मिलेगी। स्वयं प्रयास करने से आपको शिक्षार्थी के अनुभवों के भीतर झांकने का मौका मिलेगा, जो परोक्ष रूप से आपके शिक्षण और एक शिक्षक के रूप में आपके अनुभवों को प्रभावित करेगा। जब आप तैयार हों, तो अपने विद्यार्थियों के साथ गतिविधियों का उपयोग करें। पाठ के बाद, इस बात पर विचार करें कि गतिविधि कैसी हुई और उससे क्या सीख मिली। इससे आपको सीखने वाले विद्यार्थियों पर ध्यान केंद्रित रखने वाला अधिक शैक्षिक वातावरण बनाने में मदद मिलेगी।
गतिविधि 1: स्थापित और स्वीकृत तथ्यों की एक उपयोगी सूची बनाना
अपने विद्यार्थियों को यह बताएँ कि तालिका 1 में ऐसे कुछ स्थापित और स्वीकृत कथनों की सूची दी गई है, जो विद्यालय के गणित में उपयोगी होते हैं। ध्यान दें कि पहली पाँच पंक्तियाँ ज्यामिति के पिता कहे जाने वाले प्राचीन यूनान के प्रसिद्ध गणितज्ञ यूक्लिड के ’सामान्य मतों’ से लिए गए हैं, जो उनकी पुस्तक तत्व में दिए गए हैं।
| स्थापित या स्वीकृत कथन या तथ्य | एक उदाहरण लिखें या बनाएँ | जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है–... |
|---|---|---|
| ऐसी चीज़ें जो समान चीज़ों के बराबर होती हैं, वे एक–दूसरे के भी बराबर होती हैं (समतुल्यता का सकर्मक गुणधर्म) | ||
| जब समान चीज़ों को समान चीज़ों में जोड़ा जाता है, तो परिणाम भी समान होते हैं | 7 + 3 = 4 + 6 23 – 4 = 19 – 0 अतः: 7 + 3 + 23 – 4 = 4 + 6 + 19 - 0 | |
| जब समान चीज़ों को समान चीज़ों में से घटाया जाता है, तो शेषफल समान होता है | ||
| पूर्ण संख्या अपने किसी भी भाग से बड़ी होती है | ||
| किसी भी बिंदु पर कोणों का योग 360° होता है | 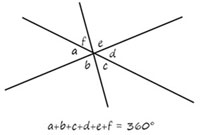 | सरल रेखा का कोण 180° होता है |
| जब कोई रेखा कई समांतर रेखाओं को काटती (या गुजरती) है, तो लंबवत रूप से विपरीत कोण बराबर होते हैं और संगत कोण बराबर होते हैं | 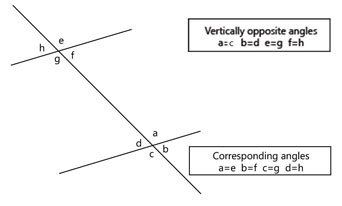 | एकांतर कोण बराबर होते हैं |
| यदि दो रेखाएँ एक–दूसरे को काटती हैं, तो लंबवत रूप से विपरीत कोण बराबर होते हैं | ||
अपने विद्यार्थियों से निम्न प्रश्न पूछें:
- क्या आप इनमें से किसी को पहचानते हैं? उनका जो मतलब हो सकता है क्या आप ऐसा चित्र बना सकते हैं?
क्या आप ऐसे अन्य स्थापित और स्वीकृत कथन जानते हैं, जिन्हें इस सूची में जोड़ा जा सकता है?
कथनों को पुनः देखें और सोचें: ‘जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है ... इन्हें लिख लें। आप अब स्वयं के गणितीय कथनों की खोज कर रहे हैं!
- अपने साथी से अपने काम और अपनी सोच की चर्चा करें, और उन्हें विश्वास दिलाने का प्रयास करें कि आप सही हैं!
गतिविधि 2: यह सिद्ध करना कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है
अपने विद्यार्थियों को बताएँ कि समांतर रेखाओं को काटने वाली रेखा के कोणों संबंधी तथ्य इस बात को सिद्ध कर सकते हैं कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
(इस गतिविधि के लिए केस स्टडी 1 को पढ़ना आपके विद्यार्थियों के लिए मददगार हो सकता है।)
अब अपने विद्यार्थियों को बताएँ:
ऐसे सभी साक्ष्यों को साथ में रखें। अपने विचार में मदद लेने के लिए वाक्य ‘जब मुझे यह पता चलता है, तो मुझे वह भी पता चल जाता है ...’ का उपयोग करें।
- अपने साथी से अपने काम और अपनी सोच की चर्चा करें, और उन्हें विश्वास दिलाने का प्रयास करें कि आप सही हैं!
केस स्टडी 2: श्रीमती अग्रवाल गतिविधि 1 और 2 के उपयोग के बारे में बताती हैं
यह एक अध्यापिका की कहानी है, जिसने अपने माध्यमिक कक्षा के विद्यार्थियों के साथ गतिविधि 1 और 2 को आजमाया।
चूँकि विद्यार्थियों के पास काम करने के लिए कुछ उदाहरण थे, इसलिए उन्हें यह आरेखित करने में प्रसन्नता हुई कि कथनों का क्या मतलब हो सकता है। उन्हें यूक्लिड के सामान्य मतों को समझने में थोड़ी परेशानी हुई और इससे एक रोचक चर्चा निकली कि जिस गणितीय भाषा के संपर्क में आए, वह तुलना में इतनी अस्पष्ट नहीं थी!
रानू ने पूछा कि ‘∠A = 30° और ∠A = ∠B तो ∠B = 30°’ जैसा कुछ ’ऐसी चीज़ें, जो समान चीज़ों के बराबर होती हैं, वे एक–दूसरे के भी बराबर होती हैं’ कथन के लिए सही माना जा सकता है। मैंने इसपर स्वीकृति या अस्वीकृति नहीं दी, क्योंकि मैं चाहती थी कि रानू यह तय करे कि क्या यह सही होगा। मैंने उसे दुहराते हुए उत्तर दिया, जो कार्य में इसने कहा थाः
’जब आपको यह पता चलेगा, तो आपको और क्या पता चलेगा?’
- ’प्रयास करें और अपने साथी को विश्वास दिलाएँ कि आप सही हैं।’
गतिविधि 2 के लिए मैंने सुझाई गई विधि का उपयोग किया। सबसे पहले मैंने उनके सामने श्रीमती कपूर की कक्षा का केस स्टडी जोर से पढ़ा; फिर मैंने चिंतन के विचार से प्रश्न पूछेः ’कक्षा, क्या आपको लगता है – क्या आपको यकीन है कि ये विचार गणितीय प्रमाण हैं? क्या प्रधानमंत्री को विश्वास होगा? क्या उन्हें विश्वास होना चाहिए?’ ऐसा करने के पीछे मेरे कारण यह थे कि यदि मैं उनसे कहती कि सिद्ध करो कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है, तो वे उन्हीं प्रमाणों को गिनाते जो श्रीमती कपूर की कक्षा के बच्चों ने बताए थे और मैं यह बताते हुए शुरू करना चाहती थी कि इन्हें प्रमाण नहीं माना जा सकता। अधिकांश बच्चे पहले इस बात से सहमत थे कि श्रीमती कपूर के विद्यार्थियों ने जो बताया था, वे विश्वास दिलाने वाले प्रमाण थे, लेकिन कुछ विद्यार्थी आश्वस्त नहीं थे। मैंने उनसे पूछा कि ऐसा क्यों, तो उन्होंने कहा कि उन्हें यह विश्वास नहीं है कि ये प्रमाण स्थापित या स्वीकृत तथ्यों पर आधारित हैं। इससे अनुभवसिद्ध साक्ष्य के बारे में चर्चा निकली, यह क्या थे और इन्हें गणितीय प्रमाण क्यों नहीं माना गया।
उसके बाद ही मैंने गतिविधि 2 बताई और विद्यार्थियों को इसके साथ खेलने, चीज़ें आजमाने और परीक्षण करने को कहा। इससे वे सहज हुए और उन्होंने अपने विचारों पर चर्चा करके और अपने तर्कों को अपने पड़ोसियों के साथ आजमाकर खुशी–खुशी इस पर काम किया। बाद में, हमने उनके विचारों पर पूरी कक्षा के साथ चर्चा की। कुछ प्रमाणों पर पूरी कक्षा को विश्वास नहीं हुआ, लेकिन कई विद्यार्थियों ने अपने प्रमाण के लिए ठोस आधार तैयार किया था।
मुझे कुछ ऑनलाइन वीडियो भी मिले, जिनमें प्रमाण दिखाई देता है, जैसे खान एकेडमी द्वारा तैयार वीडियो {नीचे ‘अतिरिक्त संसाधन’ देखें}। यद्यपि मैं इन्हें कक्षा में दिखा न सकी, लेकिन मैंने विद्यार्थियों को इनके बारे में बताया, ताकि उन्हें इनकी जानकारी रहे।
अपने शिक्षण अभ्यास में दिखाना
जब आप अपनी कक्षा के साथ ऐसा कोई अभ्यास करें, तो बाद में बताएं कि क्या ठीक रहा और कहां गड़बड़ हुई। ऐसे सवाल की ओर ध्यान दें, जिसमें विद्यार्थियों की रुचि दिखाई दी हो और वे काम कर पाए और वे जिनका आपको स्पष्टीकरण करने की आवश्यकता हुई। ऐसी बातें ऐसी ’स्क्रिप्ट’ पता करने में सहायक होती हैं, जिससे आप विद्यार्थियों को शामिल कर सकें और विद्यार्थी गणित को रुचिकर और आनंददायक पा सकें। यदि वे कुछ भी समझ नहीं पाते हैं तथा कुछ भी नहीं कर पाते हैं, तो वे शामिल होने में कम रुचि लेंगे। जब भी आप गतिविधियां करें, इस चितंन पर आधारित अभ्यास का उपयोग करें, इस बात पर ध्यान देते हुए, जैसे श्रीमती कपूर ने किया था, कि कुछ छोटी–छोटी चीज़ों से काफी फर्क पड़ा।
विचार के लिए रुकें ऐसे चिंतन को गति देने वाले अच्छे सवाल हैं:
|
2 क्या यह प्रमाण है?
