4 Using a number line to develop understanding of place value
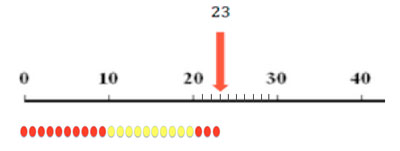
A number line provides a very strong visual image to help develop students’ understanding where any given number is positioned in relation to other numbers of place value. For example, Figure 3 shows the position of the number 23 on the number line, and also its size relative to other numbers, for example 67. The number line also shows that the number 23 is made up of 20 plus 3 (or two lots of ten plus three).

When you are working with your class, you might want to point to various points along a similar number line and ask them to estimate which number you are pointing to. Alternatively, students could work in pairs with their own number lines and challenge each other to estimate numbers and justify their answers.
Another excellent resource to use, either on its own or alongside a number line, is a string of beads. By making up the beads in sets of ten in alternating colours, the number 23, for example, can be illustrated even more clearly than on a number line to consist of two lots of ten plus three (see Figure 4). Making strings of beads is something that many students enjoy, so perhaps you might think about setting up a combined mathematics and craft lesson. This could produce some very useful resources for future lessons on counting and place value.
Figures 5 and 6 below illustrate how the use of number lines to support understanding of place value might be extended for larger numbers as well as for decimals:


These examples are just a few ways that you might be able to use number lines to support students’ understanding of place value in your classroom. No doubt you will be able to think of many more. As well as preparing number lines for specific lessons, or drawing them on the blackboard, it is very useful to have some number lines displayed on the classroom wall more permanently.
Activity 3: Planning a lesson using structured resources
For this activity you will plan a lesson using ideas from this unit. To help with this, you may want to have a look at Resource 5, ‘Planning lessons’.
Start by thinking about the students in your class, and their current level of understanding about place value. Based on this, plan a lesson that aims to build on this understanding and take it forward. You may wish to concentrate on some of the approaches described in this unit, or you may wish to also include some of your own ideas. However, you have to use one of the resources discussed in this unit. Here are just a few important points to consider:
- Be clear about which aspect(s) of place value you want the students to particularly focus on.
- Make sure that all of the students are engaged actively in the lesson.
- Provide opportunities for the students to engage in mathematical discussion with you and with each other.
- There’s no need to stick to just one particular resource in the lesson. Number lines, for example, work effectively alongside all of the other resources you have read about in this unit.
- How will you assess students’ progress through the lesson?
Then carry out your plan in your class.
Once again, after the lesson, set aside some time to reflect on what went well and why, and what you might change the next time you plan a similar lesson. You may find it helpful to use the same questions as before to structure your reflection.
Video: Planning lessons |
Case Study 2: Understanding zeros in a lesson
For Activity 3, Mrs Aparajeeta decided to plan a lesson to help her students understand the concept of zero as a placeholder using base ten blocks. This is the story of how she carried out her plan in her class using activities and resources that the students were familiar with, but with a different focus.
I started by asking three students to each hold up a large base-ten ‘hundred’, and another five students to each hold up a ‘one’.
I asked them ‘How many hundreds do we have?’ The correct response was given, and I chose another student to stand behind the three students and hold up a large card with ‘3’ written on it. I did the same for the ones. I then wrote ‘35’ on the blackboard and said, ‘That doesn’t look quite right to me. What do you all think?’
One of the students, Ram, pointed out ‘You have written 35 but the number should be 305 – you need a zero’. I had also prepared large cards with all of the digits from 0 to 9, and asked Ram to come to the front to stand between the other two groups and to hold up the zero card (Figure 7).

I explained to them why zero was a very important part of the decimal number system. For the number 305 the zero was needed to show that there are no tens. I represented the number on the blackboard to highlight this:
| Hundreds | Tens | Ones |
| 3 | 0 | 5 |
I then repeated the same process to make some more numbers with the students (for example 308, 230 and 200), and recorded them on the place value board. Each time I stressed that ‘we need the zero to show that there are no …’
For the rest of the lesson I repeated the same activities that I used in the base-ten lesson [described in Case Study 2], but this time mainly asked the students to use the base-ten blocks to represent numbers containing a zero, and also included zero cards for the game at the end of the lesson.
I was again very pleased at how enthusiastically the students had taken part in the lesson. I also noticed that doing the same activities again but with a different focus was very successful, because the students were already familiar and confident with what they needed to do.
Pause for thought
|
3 Using structured resources: base-ten blocks
