4 Meanings of addition and subtraction processes

Addition and subtraction are mutually inverse mathematical operations. For example:

5 + 1 = 6

6 – 1 = 5

6 – 5 = 1

According to some researchers (Linchevski and Williams, 1999; Bruno and Martinon, 1999) subtraction skills assist students to learn the concept of ‘negative numbers’. The processes of addition and subtraction become interchangeable in the case of integers. For example:

3 + 5 = 8 = 3 – (–5)

The next activity aims to help your students focus on the thinking processes involved in calculating positive and negative numbers.

Activity 3: Adding positive and negative numbers

Part 1: Using the ‘counters’ model to understand addition and subtraction with negative numbers

For this activity you will need a quantity of counters or pieces of card in two different colours. One colour should feature positive signs and the other colour should feature negative signs. An important part of this activity is getting students to talk about addition and subtraction with negative numbers and to explain their thinking. When you are planning your lesson you may want to have a look at Resource 2, ‘Talk for learning’.

Tell your students that all of the following arrangements of counters add up to four.

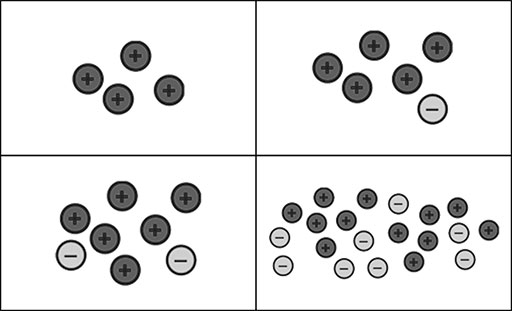
Figure 3 Various arrangements of counters that add up to four.
  • Ask the students to suggest some other possibilities.
  • Then ask them to explain how all these representations represent 4.
  • Now use positive and negative counters to represent –2 in lots of different ways, starting with just two ‘negative’ counters. Be sure to ask the students to make suggestions themselves.
  • Can they explain why all the different representations represent –2?

Part 2: Using the ‘counters’ model for larger numbers, in small groups

Put your students into small groups and tell them:

  • Using counters or pieces of coloured paper, choose a number under ten and make at least four representations of that number using positive and negative counters.
  • Record your representations as addition sums.
  • Choose a negative number and do the same.
  • If you have time, choose another number that you think will challenge you.
  • Write out the sums for each of your representations.
  • Swap with another group to mark them.

If you can, go to the NRICH website to find several more ways to develop ideas for using positive and negative counters.

(Source: Part 1 adapted from NRICH, undated.)

Video: Using local resources

Case Study 3: Mrs Nagaraju reflects on using Activity 3

I used the positive and negative counters with my class as they were having difficulty understanding how to work with negative numbers. I started off with some paper plates with positive and negative signs on them and got the students to hold the plates at the front of the class.

They came up with some good ideas of combinations that made 4. It took longer for them to start making suggestions for negative 2 but they soon did. I wrote the total number of positives and the total number of negatives on the blackboard and then asked the students for the sign that meant put them together. They quickly suggested the ‘add’ sign.

I put the students into groups of six for the next activity because there were nearly 60 in my class and they worked well together. Each group had ten pieces of paper in two colours and they wrote the positive and negative signs on for themselves. They made three different representations for each number they chose and I also made sure that they chose different numbers to the neighbouring groups. They wrote their addition sums on pieces of paper that we stuck on the wall so that everyone could see.

I wanted to see if I could use the same ideas to help them understand what happens when you take away a negative, and of course you can! I got out the paper plates again and made 5 from 8 positives and 3 negatives. I asked what number we got when we took away 2 negatives and they could all tell me the answer was now 7.

I wrote on the blackboard:

5 – (–2) = 7

For homework I asked them to look in their textbook for three similar examples like 5 – (–2) = 7 and to make a counter drawing of what these sums could look like.

Pause for thought

In the case study, Mrs Nagaraju asked a question to the whole class about which sign was needed to put the combinations together. The correct answer was given, but do you think she could be sure that this point was understood fully by all of the students? What other strategies might she have used to ensure that all of the students were involved in thinking about and discussing the answer?

Now think about the following questions:

  • When you carried out Activity 3, what questions did you use to probe your students’ understanding?
  • Did you feel you had to intervene at any point?
  • Were there any points that you feel some or all of your students need to revisit to secure their understanding?

3 Using number lines to develop understanding of positive and negative numbers

5 Summary