3 Reading multiplying and dividing fractions differently to help understanding
When you look at mathematical problems in a textbook, they can look daunting. To students, they may look like a string of alien symbols that are supposed to make sense – a feeling that can be very intimidating! This is not restricted to operations on fractions. The examples do make sense once you engage with the writing and the deciphering of the mathematical symbols.
When asked to multiply or divide fractions, it is even harder to think about what that might actually mean visually than with addition and subtraction. A way to help students overcome that sense of feeling overwhelmed by the symbolic notation of multiplying and dividing fractions is by thinking how a mathematical sentence can be read differently.
For example, the sum can be read as:
- ‘One third times one sixth’
- ‘One third multiplied by one sixth’
- ‘One third of one sixth.’
Similarly, ‘’can be read as:
- ‘One third divided by one sixth’
- ‘One third shared between one sixth’
- ‘How many sixths are there in one third?’
The beauty of mathematics is that you can decide which way works best for you to read mathematical sentences. You can then pick the way that is most conducive to working out the mathematical question – and finding the answer.
The expressions ‘one third of one sixth’ and ‘how many sixths are there in one third?’ are more conducive to thinking of a visual picture of multiplying and dividing fractions. The next activity asks the students to explore this.
Activity 2: Picturing multiplying and dividing fractions
Part 1: Making a dictionary
As for Activity 1, it is very important to allow your students plenty of time to work on each part of this activity.
Ask the students to discuss and write down as many different ways as they can think of for saying the following mathematical sentences:
- 2 × 3
- 7 × 8
Some of the answers could be:
- ‘… times …’
- ‘… multiplied by …’
- ‘… of …’
- ‘… lots of …’
Ask the students to do the same for:
Write the answers on the blackboard and leave it there for the next parts of this activity. Some of the answers could be:
- ‘… divided by …’
- ‘… shared between …’
- ‘how many … are there in …?’
Part 2: Picturing multiplication of fractions
In this part of the activity, you will ask your students to work in pairs or groups. To help with planning, you may wish to look at Resource 3, ‘Using pair work’.
Write the following multiplications on the blackboard, next to the answers from the previous part of this activity:
Now do the following:
- Ask the students to work in pairs or groups, and draw a picture that would show these multiplications in a rectangle with a length of 6 cm and a height of 2 cm – as they did in Activity 1. Point out to them that the answers still on the blackboard from Part 1 can help them.
- Tell them their ideas will be discussed with the whole class in ten minutes, and that the they do not need to have finished all the examples.
- After ten minutes, discuss their ideas and ask some of the students to come and draw their pictures on the blackboard.
- Discuss any misconceptions.
- Then ask the students to draw pictures for all the examples.
- If they finish early, ask them to make up some examples of their own.
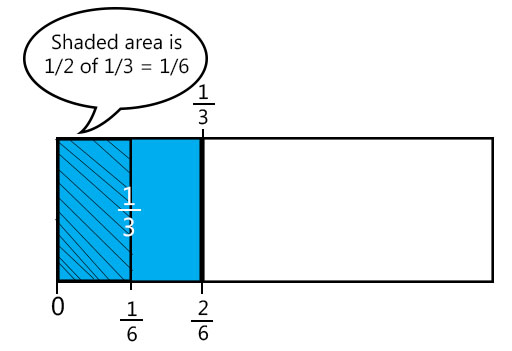
(Note for teacher: to draw a picture of these multiplications, the students think of these as ‘… of …’. So for example, for , the students would first shade in of their rectangle and then say ‘I need to find one half of this’, thereby halving the shaded third. If they have done Activity 1, they should be able to see that this equals of the rectangle.)
A solution for could look like Figure 3:
Part 3: Picturing division of fractions
Preparation
Fraction strips are very useful for this activity. You can find some example blank fraction strips in Resource 4. You can ask the students to write in the fractions that these strips represent.
The activity
Write the following division sums on the blackboard, next to the answers from the previous part of this activity:
Then complete the drawing in the same way as Part 2.
(Note for teacher: Visualising how to divide a fraction by a fraction is hard. The important thing is to remember that division means many things, but in this case you are asking ‘how many … are there in …?’ So for , you are asking how many s are there in a . Draw a square or rectangle, divide it into ½ and cut out one of these halves. Draw the same square or rectangle, divide it into quarters cut them out. How many quarters are there in one half? Easy – there are two! The sum divided by can be tackled in the same way, as can some seemingly harder sums such as divided by . But you will soon run out of fraction division sums that can easily be visualised. However, the students will by now have developed some conceptual understanding of dividing fractions and can use their procedural knowledge for the harder sums.)
Video: Involving all |
Case Study 2: Mr Aparajeeta reflects on using Activity 2
I do get disheartened when so many of my students manage to get the rules for multiplying and dividing fractions all mixed up, especially when it is on a test or exam. Some students remember how to do it, but so many do not. So I decided to give this activity a go. Because visualising multiplying and dividing fractions was new to me, I first had a go at doing the questions in the activity myself and then with my sister at home. I really got enthused by this, and then shared the activity with two of my colleagues at school. So by the time I tried it out with the students, I knew what could happen.
What I learned from trying it out myself is that I needed some time and opportunity to experiment and play with the drawing, colouring in and cutting out of the fractions. So when I did it with my students I made sure I gave them sufficient time to do the same, and not to rush. I think building an image in your head takes time, especially when it is new to you.
The students seemed relieved to find out that multiplying and dividing fractions actually meant something – that you could see what it means and that you could say what it means. It made me realise that mathematical notation and symbols are different from ‘normal’ text, and that not much attention is paid to learning to read and interpret mathematical symbols.
For all the parts in the activity, the students worked in pairs. I thought that would work well for the experimenting and give students some time to think for themselves quietly.
I used the fraction strips [see Resource 4]. Because we do not have a photocopier at school and I did not fancy drawing fraction strips for so many students – I have more than 80 in my class – I planned for this and asked each student to make these at home using paper from their exercise books the night before. Of course, some had forgotten to do it or bring it in, but we had enough so that each pair of students had at least one set of fraction strips.
There were two girls in the class I had been getting worried about before – they always seemed so anxious in maths lessons, never putting their hand up and always looking at what other students were doing. I asked them to work together as a pair on this. At first they were not engaging with the activity at all, and looked at other students to see what they were doing. But after about four minutes they started to have a go, and they started talking to each other as well. They seemed to relax. In the whole-class discussion I asked one of them for their ideas and they answered, although in a quiet voice. A first step!
Pause for thought
|
2 Issues with learning about operations on fractions
