2 Learning about variables and constants through talking
A very efficient way for students to develop understanding and give meaning to any mathematical concept is through talking:
Children need to learn how to … use mathematical language to create, control and express their own mathematical meanings as well as to interpret the mathematical language of others.
(Pimm, 1995, p. 179)
Students who do not learn how to ‘talk mathematics’ lose out on many things; in particular, as Pimm says above, they do not have the resources to available to create, control and express their own mathematical ideas.
Encouraging students to talk about mathematics and helping them to develop appropriate vocabulary and phraseology to do so is an important part of learning. Thinking and communicating are so intimately entwined (Sfard, 2010) that it is not possible to know where one stops and the other starts. If you want your students to think about, understand and therefore effectively learn mathematics, they will also need to learn to communicate their mathematical ideas.
Students will also be able to talk about what they are thinking with one another. The act of forming thoughts in order to communicate with another can enable misunderstandings to be corrected. Thoughts that have to be formed into something that can be communicated, have been shown to be much more susceptible to recall by students (Lee, 2006); in other words, they are more likely to have learned those ideas.
The first activity asks students to think about identifying quantities in their experiences from their real life. It uses a picture to trigger their imagination. The activity suggests giving a short time limit for students to come up with their ideas to give a sense of urgency, competitiveness and excitement. This also means they will have little time to worry about doing algebra.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all, or at least part, of the activities yourself. It would be even better if you could try them out with a colleague as that will help you when you reflect on the experience. Trying them for yourself will mean you get insights into a learner’s experiences which can, in turn, influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students and, once again, reflect and make notes on how well the activity went and the learning that happened. This will help you to develop a more student-focused teaching environment.
Activity 1: Pictures are worth a thousand words
Preparation
This activity is done best in pairs or small groups. Make sure the students in the group are seated so that they can hear each other well. If you feel the students need some more time at any point, give them some bonus or extra time. You may want to look at the key resource ‘Using pair work [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] ’.
The activity
Ask your students the following:
How many of you have travelled in an autorickshaw? Figure 1 shows Mr Murti travelling in an autorickshaw. In your groups, think of as many (measurable) quantities as you can that are associated with an autorickshaw ride. The group who writes the greatest number of such quantities in four minutes will be the winner. Your time starts … now.
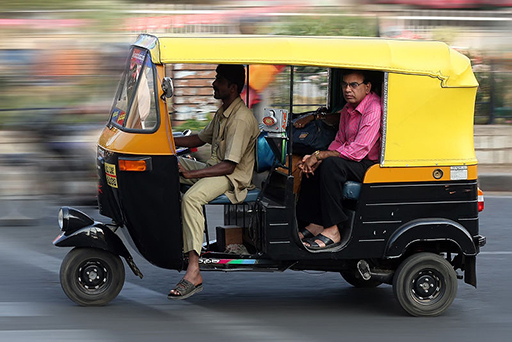
Then, ask for their ideas to share with the rest of the class. This could be organised as follows:
- At the end of the time limit, ask them to put their pencils down.
- Give them ten seconds to count the number of things they wrote.
- Now choose the group which wrote the minimum and the group which wrote the maximum number of quantities.
- Ask two students of the group that wrote the least number of quantities and two students of the group that wrote the most to come and write the quantities they thought of on the blackboard simultaneously – this will save time. Ask the students to stay at the blackboard.
- Ask each group in the class to share any other quantities they came up with that are different to those already on the blackboard. Ask one of the students at the blackboard to write down each of the new suggestions. Having so many scribes at the blackboard at once means that this can be done quickly.
- Soon, you will have a lot of quantities related to an autorickshaw ride on the blackboard. Some of these may include:
- number of passengers
- total fare for a journey
- time taken for a journey
- number of red lights at traffic signals during the journey
- distance of a journey
- number of wheels on an autorickshaw
- number of bolts on each wheel of an autorickshaw
- registration number of the autorickshaw
- speed of the autorickshaw
- cost of the autorickshaw
- mileage of the autorickshaw.
If you can, leave this list on the blackboard and ask your students to copy it. They will need it for Activity 2.
Video: Using pair work |
Case Study 1: Mrs Bhatia reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with his elementary students.
I myself sometimes get confused about variables and constants, and how they relate to each other, so on the one hand I thought it would be good for my own subject knowledge development to do these activities in the class, on the other hand that made me feel a bit fearful. What would happen if I got confused in the class, in front of my students?
So I did Activities 1, 2 and 3 first on my own, and then with a colleague during a lunch break. The difference between doing them on my own, and with my colleague, is that we could talk together, and help each other when something was not clear in our understanding. And also, together we came up with so many funny examples meaning we laughed a lot doing algebra! Having a go at it first made me feel very well prepared to do these activities in class.
To introduce Activity 1, I showed the students the picture of Mr Murti, and I asked them to tell the class a little bit about their own journeys in an autorickshaw. That actually helped getting some extra variables to think about, such as: how far it was to Auntie Anju’s house, how far to the park, the different number of passengers on these journeys, the time it took and how this varied whether the roads were clear or a bit flooded from the monsoon rains. Only then did I ask them to do the activity.
I asked them to work in groups of four. Telling them they had only four minutes really spurred them into immediate action and there was a sense of competitiveness and eagerness. However, I also think that by giving them only four minutes I gave the students who are a bit shy an excuse to not really contribute much. Perhaps next time I will give them a bit longer and the extra instruction of making sure that everyone in the group has contributed at least two ideas.
To feedback to the class, I used the approach that is suggested in the activity. The big advantage of it was that we had loads of examples on the blackboard in record time while still valuing the contributions of the whole class. I thought that was a good idea – I have about 90 students in the class and so I often avoid ‘sharing with the whole class’ because it takes so much time.
Reflecting on your teaching practice
When you do such an exercise with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and being able to progress, and those you needed to clarify. Such reflection always helps with finding a ‘script’ that helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting as Mrs Bhatia did some quite small things that made a difference.
Pause for thought Good questions to trigger reflection are:
|
1 Variables and constants in school mathematics
