2 Visualisation for developing understanding of algebraic identities

An effective way to rely less on memory for learning is through the use of visualisation. Visualisation means seeing an image of something in your mind. Different people will not always ‘see’ things in the same way, but ‘visual thinking’ is very important to the construction of understanding by your students (Dörfler, 1991).

Visualisation can be introduced with relatively simple operations. For example, multiplication can be represented as a product table that is similar to area. (There are other ways to represent multiplication.)

The product 7 × 3 can be represented by an area of seven by three squares (Figure 1). From this image it is also clear that multiplication is commutative – that is, the product of 7 × 3 is the same area as the product of 3 × 7.

Figure 1 A product table for the sum 7 × 3.

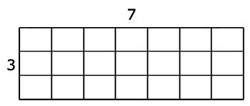
So 7 × 3 is equivalent to 3 × 7 is equivalent to 21. This can be written as:

7 × 3 ~ 3 × 7 ~ 21

Modelling multiplication can help your students to understand a multiplication problem, because the area of a large rectangle can be easily decomposed into areas of smaller rectangles. It is good practice not to draw the area models in proportion to the numbers used: it stimulates more abstract representations and makes the mental jump to representing negative numbers less difficult. Because it is not possible to have a negative area, this kind of representation is referred to as a ‘product table’.

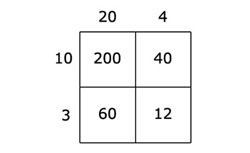
For example, 24 × 13 can be represented by the product table in Figure 2. Hence 24 × 13 ~ (20 + 4) × (10 + 3) ~ 200 + 40 + 60 + 12 ~ 312.

Figure 2 A product table for the sum 24 × 13.

In another example, 19² can be represented by the product table in Figure 3. Hence 19² ~ (20 - 1) × (20 - 1) ~ 400 - 20 - 20 + 1 ~ 361.

Figure 3 A product table for the sum 19².

This decomposition model is very helpful for finding products of larger numbers or for multiplication involving algebra. A simple example involving algebra is 3(a - b), as shown in Figure 4. Hence 3(a - b) ~ 3a - 3b.

Figure 4 A product table for 3(a – b).

You might have noticed that in these examples the equivalence sign (~) has sometimes been used instead of the equals sign (=), which would be equally valid. The equivalence sign can offer a certain freedom, playfulness to mathematics, in particular if the sign is read as ‘is another way of saying’ instead of ‘is equivalent to’.

Activity 1 will support students in working with visualisation by seeing multiplication as a product table. Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, because that will help you when you reflect on the experience.

Trying the activities yourself will mean you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, read Case Study 1 and use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.

Case Study 1: Mrs Aparajeeta reflects on using Activity 1

This is the account of a teacher who tried Activity 1 with her secondary students.

Before starting on this activity we had a discussion on how a number that is squared or multiplied could be represented by an area model, mimicking the way I learned it from reading this unit. I started with small numbers like 5 x 6 and then to bigger numbers like 56 × 64 and 65 × 115. Anup thought of using the distributive property for the question 65 × 115 = 65(100 + 10 + 5), and so he went ahead and represented it as a one-by-two table [Figure 5].

Figure 5 A product table for the sum 65 × 115.

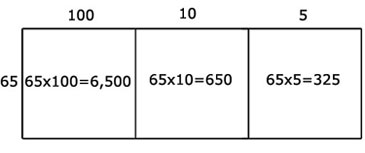
We then tried the other multiplication problems. They worked on this mainly on their own, although every now and then I could see students looking at their neighbour’s work. They could do most of them well. With the decimal question, most of them distributed it as 14 + 0.3. I asked them if they felt it was now simpler and some of them said that it was not, so I told them that they could think of a further decomposition to make a three-by-three table.

When they came to 98², the ones who decided on 90 + 8 had no problems, but one of them decided to represent it as 100 - 2 so then he wanted to know how an area could be negative. This led to a lively discussion about representation and modelling in mathematics and why it can be helpful to come up with different labels. In this case, the difference and sameness between a product table and an area representation. We conjectured that the product table and the area representation would be identical when working with positive numbers, but you would have problems with negative numbers in the area model because a negative area does not actually exist. However, we know a product can be negative, so that is why we would call it a product table!

I did not go deeper into the 100 - 2 representation itself, but it led nicely into discussing the next part of this unit: how to deal with negative numbers in a product table.

Pause for thought Good questions to think about after the lesson are: How did it go with your class? What responses from students were unexpected? Why? What questions did you use to probe your students’ understanding? Did you feel you had to intervene at any point? What points did you feel you had to reinforce? Did you modify the task in any way? If so, what was your reasoning for this?