3 Algebraic identities seen as special cases of multiplication
Students often perceive algebraic identities as some magic or a gospel truth. They rarely develop a sense of where these identities appear from or that they are special cases of multiplication.
One of the reasons why students tend to memorise identities is that they fail to associate any meaning with the relationship being depicted by the identity. You may have noticed students making common errors when they recall identities such as:
Even though it is fairly simple to check if the two statements are correct (all that is needed is to verify them for a few values of the variables), students continue to make these mistakes. Sometimes students are not aware of how easily they can verify their statements. Another and more serious reason is that they have never understood the physical (or geometric) meaning of these statements.
You can use the visualisation techniques you introduced in the previous section to help your students to understand these identities. Activity 2 gives you a method to help your students discover for themselves the meaning of different identities. The task focuses on finding, seeing and generalising the patterns of algebraic identities. Students work with a partner, as talking about the ideas helps to develop their understanding.
Before beginning this activity, it would be a good idea to first check your students can illustrate the lengths x + y and x - y correctly. The former is easier to conceive and the latter may take a bit more effort.
Illustrating the length ‘x + y’
If the white portion is x, and the grey portion is y, then the black portion is x + y. This could also be described as ‘the length of the white portion (representing x) added to the length of the grey portion (representing y) is the same as the black portion (representing x + y’ (see Figure 6).
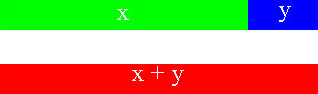
Illustrating the length ‘x – y’
If the white portion is x, and the grey portion is y, then the black portion is x - y. This could also be described as ‘the length of the white portion (representing x) take away the length of the grey portion (representing y) leaves the black portion (representing x - y)’ (see Figure 7).

Activity 2: Algebraic identities as special cases of algebraic multiplications
Tell your students the following:
- Describe (not draw or work out) the following mathematical expressions as a product table to your neighbour. What would it look like?
- a.(x + y)2
- b.(x + a)(x + b)
- c.(x − y)2
- d.(x − y)(x + y)
- Now draw the representation of each expression as you have described it in Step 1 as a product table.
- Try to write the mathematical expression that represents the areas you have drawn in Step 2 in a different way.
- Observe and compare your answers to Steps 1, 2 and 3 for each of the following four expressions:
- How many terms do you get for the expressions (a), (b), (c) and (d) in Step 3?
- How are these terms formed?
- What is the same about these expressions? What is different? It might help if you colour in the area boxes corresponding to the terms.
- Describe a rule or method for working out the algebraic identities in this way so other students in other classes could read about it.
Case Study 2: Mrs Kapur reflects on using Activity 2
Because I thought there would be some students who would find moving from number to algebra confusing, we did the first question, (x + y)2, as a whole class activity. Because of this, and because the students had already made product tables in Activity 1, the students could do Steps 1 and 2 fairly easily.
Step 3 led to a discussion about the significance of equivalence. An expression with collected terms can be equivalent to one where the terms have not been collected yet – it just looks a bit messier somehow! I asked them whether they could come up with some ideas to make it look even more messy, and they had great ideas! It made us all laugh, which was really nice, especially as the students who are normally very quiet and perhaps have some mathematics anxiety also smiled and looked more relaxed.
The last part of Step 4 proved hard. The difficulty was not in describing it, but in doing so succinctly. The descriptions we ended up with were not perfect, but the students and I were happy with them. We all realised that to improve we would simply need more practice at writing our own descriptions and methods.
We extended the questions to include (a + b + c)2 and then tried with terms being assigned different signs, and they could get the solutions easily.
We also decided that to do (a + b)3 or (a − b)3, we could do it in two parts, (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2), and then put this in the product table.
The students felt really happy and confident with working in this way. One student said that he felt so relieved that he would now be able to think of a way to work out the algebraic identities if his memory failed.
Pause for thought Good questions to think about after the lesson are:
|
2 Visualisation for developing understanding of algebraic identities
