3 Using generalisation to find misconceptions

When you see an expression like 2(3 – 8), you might spot immediately that this could be rewritten as (2 × 3) – (2 × 8), because it is an example of the law of distributivity where a(b – c) = a × b – a × c.

Spotting such patterns and generalisations is helpful in mathematics because it makes it easier to solve problems. The downside is that sometimes you might think something is a pattern and so you generalise it, when actually it is a special case and will only be true in some circumstances. The next activity gives some examples of writing generalised algebra from numerical expressions.

Activity 4: Substituting the specific with the generalised form

Tell your students the following:

  • Below are expressions and equations that are arithmetic examples of a generalised form that algebraic expressions and equations can take. Some of these are equations, not just expressions – make sure you know the difference.
    1. 2 (3 – 8)
    2. 12 + (13 + 81) = (12 + 13) + 81
    3. 2 + 2 = 2 × 2
    4. one times left parenthesis right parenthesis 14 equals four
    5. (–7) = 7
    6. 42 + 0 = 42
    7. 23 × 1 = 23
    8. 5 per cent of 120
    9. (12 + 51)/(12 × 51)
    10. 2 + 3 = 3 + 2
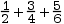
  • Write down general algebraic expressions or equations for these. There is more than one solution for some of them, so be inventive!
  • Will these always hold true? Can you say that they will be valid for any number?

Video: Monitoring and giving feedback

You may also want to have a look at the key resource ‘Monitoring and giving feedback [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] ’.

Case Study 3: Mrs Agarwal reflects on using Activity 4

Mohit spotted straight away that the first expression, 2 (3 – 8), was an example of the distributive property over subtraction, and according to him it would hold for any value of number. He gave the general form as a(b – c) = a × b – a × c.

The example of 2 + 2 = 2 × 2 led to interesting discussions and made some misconceptions come to the fore about indices and what ‘to the power of’ means when Rima said that ‘= 22’ could be added to that equation. Questions 6 and 7 made the students think about identities and some were surprised that these were not the same for all operations – they actually knew this when working with arithmetic examples, but seemed to have forgotten when using a generalised form!

Although I was happy to try out this task, I had not expected that it would offer me so many insights into students’ misconceptions. I am still thinking about why this activity lets this happen. Was it the discussion, or the ‘simple’ examples? Why does it not happen so much when doing exercises from textbooks? When I am thinking about ways that I assess my students in class, I must remember that using tasks that ask the students to apply what they know in an unusual but not necessarily difficult context lets me evaluate what they know very clearly.

Pause for thought

  • What responses from students were unexpected? Why?
  • What questions did you use to probe your students’ understanding?
  • What do you think is the reason that this task allows misconceptions to emerge as they did in Mrs Agarwal’s class?

2 Using substitution to think about possibilities

4 Summary