3 Using the question ‘What happens if …?’
Activity 1 used the question ‘In how many ways …?’ to trigger students to play, explore and investigate how any closed polygons could be made up of right-angled triangles. Having the choice of how to go about this, and make mistakes, enthused your students to engage with the task.
Playfulness involves thinking about changes in situations. This is sometimes referred to as ‘What if?’ thinking. It works very well with thinking about variables in mathematics: ‘What will happen to the other variables when I change this variable?’ In this process of thinking of possibilities, the role of and connection between, variables and constants are also discovered.
Activity 2 asks students to think about asking ‘What happens if I change …?’ They can get a sense of ownership and feeling valued for their thinking powers from coming up with their own conjectures and by using their own examples to work on. At the end of the activity, collating information based on these different examples will also allow for generalisations to be made.
The activity also asks students to first think about what is going to happen before testing their ideas. This should help them to consider what thinking is required (called ‘meta-cognition’). When their thinking proves to be right, this can make them feel good because they get it ‘right’. If their conjectures prove incorrect, this can also surprise them and make them feel intrigued about ‘Why it is that …?’
Activity 2: Students discover asking ‘What happens if …?’
This activity requires your students to explore what happens if they change a side or angle of the triangle, and to consider the effect this change has on the other angles and sides.
Part 1
Tell your students the following:
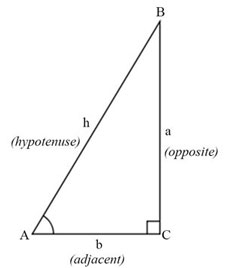
- Draw a right-angled triangle and label it as in Figure 4.
Figure 4 An example of a right-angled triangle.
- In Table 1, each row indicates a transformation to a side or an angle of the triangle that you have drawn. The blank cells need to be completed with how the other parts of the triangle will increase or decrease as a result of the transformation.
- Make a copy of the table and first write down what you think will be the change; then check by drawing the changes. If there is no change, write ‘no change’.
| Angle A | Angle B | Angle C | AB | BC | AC |
|---|---|---|---|---|---|
| Increases | Fixed | ||||
| Decreases | Fixed | ||||
| Increases | Fixed | ||||
| Decreases | Fixed | ||||
| Fixed | Doubled | ||||
| Fixed | Is halved | ||||
| Fixed | Increases | ||||
| Fixed | Fixed | ||||
| Fixed | Fixed |
- What do you notice? Why do you think this is?
Part 2
- In each row of Table 2, you are given the size of angle C and the lengths of sides AB (the hypotenuse) and AC.
- Draw these triangles and determine the values of other missing parts.
- Again, make a copy of the table and first write down what you think will happen, before checking by drawing the triangles.
| Angle A | Angle B | Angle C | Hypotenuse (AB) | a | AC |
|---|---|---|---|---|---|
| 90° | 2 | 1 | |||
| 90° | 4 | 2 | |||
| 90° | 6 | 3 | |||
| 90° | 8 | 4 |
- What do you notice? Why do you think this is?
Case Study 2: Mr Chadha reflects on using Activity 2
I introduced Part 1 of the activity by telling the students they were going to do a ‘What happens if …?’ problem that required them to be detectives and to think about possibilities. First of all they had to construct a right-angled triangle using their own measurements, which they had to first jot down. Having done that, I asked them to copy Table 1, which I had written on the blackboard.
At first they started to use the measurements of their own triangle to fill in the table and I had to remind them that they were looking for increases and decreases. This helped them to get started. I could see several of them moving their arms while squinting their eyes. When I asked Nitin what he was doing when he moved his arms, he said, ‘I am increasing the angle in my mind’s eye so I can “see” what happens to the other sides.’ I told him that was interesting and to carry on. When it came to thinking what happened to the other angles when the sides are doubled or halved, some students needed to draw the new triangle at least roughly so that they were certain. I encouraged them to ‘imagine’, to use pencils or to draw – whatever they chose to do – to ‘see’ what happens when a right-angled triangle is manipulated in this way.
Once the table was filled in, the students had to think about what they noticed. I first asked them to look at their table and think for 30 seconds; then I asked them to tell their partner what they thought they saw in the table and to agree on something that they noticed. I then asked the students to tell another pair what they had noticed and agree an idea in their group of four. Each group told the rest of the class what they had noticed and a lively discussion ensued. I felt that this made sure everyone’s ideas were discussed and included in a very short time.
Then we went on to Part 2. This time I asked them to fill in the table with what they thought would happen without any drawing at all – even in their mind’s eye! After giving them two or three minutes to do this, I asked them to work in pairs to do the drawing so that they could check what they thought was correct or not. Drawing is always difficult to do accurately, so I reminded them that the drawing was to make sure that what they thought in theory was actually the case. If they measured an angle and it seemed to be a few degrees out, I asked them to think whether it was their ‘theory’ that was likely to be ‘wrong’, or their ‘practice’. They quickly understood what I was saying and were able to argue for their own ‘theory’. I also heard several students say ‘I noticed that …’ as they were working so that they were ready for the class discussion that followed.
Pause for thought Think back about some of the features of possibility thinking from Section 1 of this unit and consider whether your students:
Which of your students especially displayed these skills? Can you give examples? |
2 The role of choice