1 Estimation is thinking about the mathematical process
As with most things in life, and like the fruit juice vendor in particular, the more you practise estimation, the better you get at doing it. The interesting question is, why is it a good idea to be a good estimator? Why do you want to encourage your students to be good estimators? What learning does estimation afford that is different from working out the exact answer?
When estimating, students can actually start to consider in detail the thinking process required to solve the problem posed, without the pressure of finding the exact answer, and without being drawn into the details of precise calculations. Applying algorithms will give an exact answer, not an estimate. Hence, estimating is making an outline of the thinking that will happen, together with a sense of the range of where a solution can lie. It can make students think about why an algorithm works. When they then later work out the exact answer to a question, they can verify whether or not their thinking was clarified in the estimation process, and thus become aware of any errors in thinking made in the calculations.
So in this way, estimating is a tool for thinking mathematically. This is especially relevant in India, because the use of calculators is not allowed in school mathematics – becoming caught up in lengthy calculations is therefore a reality.
In Activity 1 you will ask your students to first practise estimation in questions they might be more used to, but this activity also forces them to start thinking about a range of possible answers. In Question 3 of the activity you will ask them to think about estimation as a way to describe the mathematical thinking process involved in calculations using a real-life object.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.
Activity 1: Estimation and errors
Ask your students the following:
- Find the integer closest to the given numeric expressions without calculating the exact answer.
- a.
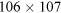
- b.
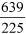
- c.
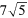
- a.
- Estimate the values of these expressions at the given values of the variables. Again, do not calculate the exact answer.
- a.Estimate the value of

- b.Estimate the value of
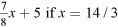
- c.Estimate the value of the expression
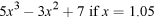
- a.Estimate the value of
- Estimate the length of the rope that is used to make a traditional cot like the one in Figure 2.

When most of your students have made an attempt at the questions, ask them:
- Can you describe what you did to answer these questions? What does estimating make you do or think? It might help to first look at what you did in Question 3.
Students may have used different approaches to the estimation. It is important to accept all their suggestions and then ask them to evaluate the different ways of doing the estimation.
Case Study 1: Mrs Aparajeeta reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with her secondary students.
Questions 1 and 2 we did as a whole class activity. I wrote the questions on the blackboard, one at a time, and then took answers and ideas from the students. For questions 3 and 4 we started off as a whole class, and then they worked on it further in pairs.
When I wrote the first question on the blackboard, the students were giving each other very doubtful looks as they had never been encouraged to do anything like this before – they wanted to simply calculate the exact answer.
Suddenly, Rachit said it would be 420,000. I asked him why he thought so and he said that 6 times 7 was 42 and we add the four zeros for the hundred times hundred. Sakshi at once said that 6 and 7 were in the units place so that would not be so, but she said that she thought it would be more than 10,000 because both 106 and 107 are bigger than 100 and 100 × 100 equals 10,000. Taruna and Rahul agreed.
Part (b) of Question 1 slowed them a bit but Taruna decided it would be more than 2 and less than 3. When asked for reasoning, she said 3 times 225 would be 675, which was more than the numerator, and twice 225 would be 450, which is less than the numerator. For part (c), Aditya decided it would be more than 14 as root 4 was 2, and so root 5 would be more than that and thus the result of the product would be more than 14.
What struck me was that in their rationale they automatically started using the language of ‘more than’ or ‘less than’. It seemed that thinking about upper and lower boundaries is actually a natural thing to do. It made me think that perhaps I should not spend so much teaching time on it, but use questions like this to make them develop these concepts naturally.
They were very doubtful about the expressions to start off with. I assumed this was because it involved a fraction – perhaps I should have asked. I waited for a little while so they would really be aware that they were stuck and they would value the hint I was going to give: to start with estimating . Shivam decided that would be around 0.8, which is almost 1, and hence that expression would be x + 5. I asked them whether that would be the maximum or minimum value, and they all agreed that it would be the maximum. For the expression involving I did not need to give any hints. They all went straight away to estimating what would be – it seemed my hint had worked. They said the value would be around 4 and this meant the minimum value would be 9.
With the third expression their faces looked worried. I asked them what worried them and they said it was the cubing and squaring. So I helped them by giving them a support question: I asked them to cube 3 and 0.1, and see the results. Taruna said that 3 cubed would be a bigger number than 3, but the cube of 0.1 would be smaller than 1. I then simply said ‘now look at this expression’ and they at once came up with answers. Again, without prompting, they identified a range in their estimations.
With the cot there was a real sense of excitement in the classroom. They asked me what the length and breadth of the cot was. I told them that their estimation started from there – it was up to them. They all decided they should take it as 2 metres by 1 metre. But there was a lot of discussion about how they would have to double, as the rope had to be wrapped around the frame. At this point I asked them to work on this in pairs, and be ready to share their thinking later on with the whole class.
Question 4 caused a lot of discussion. They found it difficult to describe this – they did not seem to have the language at first. I thought it would help them if they all could practise their talking aloud and sounding out their thoughts, so I asked them to describe their thinking to each other in pairs and when they were happy with their descriptions to write these in their exercise books. We then shared some of the descriptions with the whole class. I noticed some students made changes to what they had written as a result of that whole-class discussion. The descriptions were perhaps not very polished, but I was impressed with their attempt and commitment to start thinking about their thinking – it is not an easy thing to do! I told them that and also said that I still found it very hard to do.
Reflecting on your teaching practice
When you do such an activity with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and those that you needed to clarify. Such reflection always helps with finding a ‘script’, which helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved.
Pause for thought Good questions to trigger such reflection are:
|
What you can learn in this unit
