2 Comparing estimations with exact calculations
In Activity 1 you asked students to practise estimation and to start thinking about the mathematical thinking processes involved in the calculations. The next activity pushes this further and offers more opportunities for you and your students to focus on mathematical processes by comparing estimates with exact answers and for students to become more aware of the purpose of estimating. It uses problems where students would normally not consider estimating the answer first but move straight into working out the exact answer. This activity asks them to stop and think first.
Activity 2: Estimating as a guide
Ask your students the following:
In each of these problems, first estimate the answer (without working it out) and then work out the exact answer. Find the difference between the estimate (E) and the exact answer (A).
- How many kilograms of sugar can Mohan purchase for Rs. 500 if a kilogram of sugar costs Rs. 75?
- Temperatures in some countries are measured in Fahrenheit (°F); in India, temperatures are measured in Celsius (°C). The two measures of temperatures are related by the equation
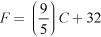. If the temperature in New Orleans, USA is 95 °F, what is the corresponding temperature in Celsius? - The area of a triangle with sides a, b and c is given by
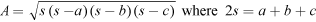. Find the area of an equilateral triangle whose side is 4 cm in length.
When the students have given an estimate and an exact answer, ask them:
Do you think your estimation was good? What could you have done to improve it? Did estimating the answer first help you at any stage in finding the exact answer?
Did your students find estimating the answer helpful? Are they confident at estimating? If not, how can you and other students help them?
Case Study 2: Mrs Kapur reflects on using Activity 2
I asked the students to work on this individually and to be ready to explain later on to the whole class how they did their estimation. We then compared answers – quite a few gave in to the temptation and found actual values. In those cases I asked them to explain what their methods of estimating would have been. This was actually really interesting, because when they were tempted to explain the estimating process as exactly the same as working out the correct answer, the other students who had done the estimation as well would comment and critique (in a friendly and constructive way, of course!).
For Question 1, Rahul said that 1 kg cost Rs. 75, so 2 kg would be Rs. 150. Rs. 300 would mean 4 kg and Rs. 450 would mean 6 kg, and because there was more money than that available, the quantity would be more than 6 and less than 7 kg.
The second question was not one they had ever tried talking about, so at first they simply would not try it – no one volunteered! So I acknowledged this might be uncomfortable for them and asked who would attempt an explanation. Sakshi and Usha, who were sitting next to each other, both put their hands up after nudging each other. I applauded their ‘bravery’ and invited them to both help each other with explaining. They explained they would take 95 to be 90 and would subtract 30 to give 60. They said that is almost 2, so dividing by two they could estimate that the Celsius would be more than 30. No one could come up with a better way to estimate. We then discussed what the effect was of first estimating on the understanding of the problem. The students felt that by hearing the description of the process of the estimation, they could suddenly see connections of how degrees in Celsius might be related to degrees in Fahrenheit.
Question 3 was interesting in that nobody, including myself, could think of a way to estimate that would be different from working out the exact answer. We then had a good discussion about why this was, and concluded that actually we did not have a picture, or a clear understanding, of what the formula of the area as was given meant, apart from that it was an algorithm.
1 Estimation is thinking about the mathematical process