3 Estimation in real life
Estimation is used in real life all the time. The NCF (2005) also recommends that mathematics be applied to other curriculum areas to improve understanding and increase the relevance of the subject, and estimation is a useful idea in many other areas.
The next activity involves engaging your students in estimating real-life quantities such as distance, areas and volumes, connecting mathematics with geography, history and local customs. The objects and scenarios used for estimation may be adapted to suit your local environment. You could also ask students to come up with examples as part of their homework. If you or your students have access to the internet, you can find lots of local information quite easily.
Activity 3: Estimation in real life
If you are doing all three activities with your class, you might want to divide students into groups and ask different groups to work on different problems. Decide if you want your groups to be students who are all confident maths learners or if you will create mixed groups.
Tell your students to get into their groups and tell them which problem to solve. You could write the problems on large pieces of paper to stick up on the walls of the classroom:
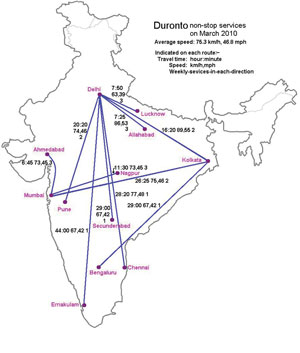
- Estimating distances: Figure 3 provides us with details of the Duronto rail services in India. For each journey between two cities you are provided with the travel time as well as the average speed of the train in km/h. Can you estimate the total distance that a person will travel if they have to visit all the cities in the network using the Duronto network?
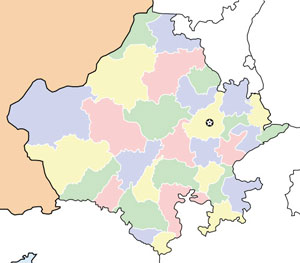
- Estimating area: Find a method to estimate the area of each district in your state (Figure 4).
- Estimating volumes: Pick any three objects that can hold different volumes of liquid. (Some examples are shown in Figure 5.) How would you estimate the volumes of water they can hold?
Figure 5 Four examples of objects that can hold liquid.
Read Resources 2 and 3, ‘Using local resources’ and ‘Using groupwork’, to find out more.
Case Study 3: Mrs Agawal reflects on using Activity 3
The first question the students came up with was ‘Are we to go to all the cities connected with Duronto network?’ So I said yes, try to go to all of them and yet travel the minimum distance possible, and that it might be really handy to keep a tab where you have been and where not. They really liked the task – they had to work out their own method of approaching it. I suggested that they make groups of four, because this might lead to finding better solutions. There was a lot of discussion about which should be the centre from where the movements could take place.
During sharing time we had a very interesting debate about what was the best way to travel and the purpose of estimation in this case. They all agreed that estimation was the only sensible way to work on this problem, as an exact answer would actually be irrelevant.
They were a bit confused at first about the area estimation in Question 2. They said they needed some more information to work on this. We discussed why this was, and what they would need. They agreed that they would be allowed to find one small bit of information that they could find from atlases or from the internet. One group went and found the area of the smallest district as they said that would help them to estimate the others. Another group decided to find the area of their own district and then estimate the areas of the others. A third group tried to find the scale of the map given and then decided to use some geometrical formulae to get to the answer. There were a variety of answers. We then added up their estimates to see which of them were closest to the actual area of their state. We discussed the purpose of estimating in this problem and the mathematical learning they gained from doing this. They all agreed that estimating was the only sensible approach, and that having to estimate the areas again and again for different shapes of states made them think about what needs to be paid attention to when calculating area.
Then came the volume question. They all picked the glass as one of the items. The reason they gave was that they knew that a litre bottle of Pepsi filled five such glasses (although some said six glasses). So they could then decide how many glasses would be needed to fill the other shapes. The answers were of course varied, as they all estimated the size of the vessels differently. But they gave good justifications for their answers, which was satisfying to me as a teacher.
Pause for thought
|
2 Comparing estimations with exact calculations