3 Coming to know mathematical properties and facts
The students of Mrs Kapur’s class came up with examples of how they could go about creating a mathematical proof. However, neither can be considered a mathematical proof because the arguments used are not all based on accepted or established statements. Although the second suggestion uses the fact that angles on a line add up to 180°, it is not ‘proof’ that the three angles would always ‘fit’. The students might argue that it just ‘works’, but such a justification is based on empirical evidence and not on the mathematical properties of angles in a triangle.
Proving theorems should be done by building on existing theorems and axioms; however, you have to know some of these first before you can start building on them! Yet once you know some, you can deduce many others from these and develop your own corollaries.
Activity 1 lists some established and accepted statements that are useful in school mathematics. Some are from classical geometry and useful in the above proof, but the examples also make clear that theorems appear in more areas of mathematics than just geometry. The task is for your students to add some more to the list, and to use their imagination and natural deduction skills write down some statements of their own that follow on from the given statements. A good phrase to use to trigger such thinking is: ‘When I know something, then I also know something else.’ By doing this, students will also make connections between different concepts and start practising their skills of deduction.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about how that the activity went and the learning that took place. This will help you to develop a more learner-focused teaching environment.
Activity 1: Making a useful list of established and accepted facts
Tell your students that Table 1 lists some established and accepted statements that are useful in school mathematics. Note that the first four rows are from the five ‘common notions’ that Euclid, the famous Ancient Greek mathematician known as ‘the father of geometry’, wrote in his book Elements.
| Established or accepted statement or fact | Write or draw an example | When I know this then I also know that … |
|---|---|---|
| Things that are equal to the same thing are also equal to one another (transitive property of equality) | ||
| If equals are added to equals, then the results are equal | 7 + 3 = 4 + 6 23 – 4 = 19 – 0 Hence: 7 + 3 + 23 – 4 = 4 + 6 + 19 - 0 | |
| If equals are subtracted from equals, then the remainders are equal | ||
| The whole is greater than any of its parts | ||
| Angles at a point add up to 360° | 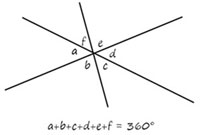 | The angle of a straight line is 180° |
| When a line intersects (or crosses) a set of parallel lines, then vertically opposite angles are equal and corresponding angles are equal |  | Alternate angles are equal |
| If two lines intersect each other, the vertically opposite angles are equal | ||
Ask your students the following questions:
- Do you recognise any of these? Can you add a drawing of what they might mean?
- Do you know any other established and accepted statements that you could add to this list?
- Look at the statements again and think: ‘When I know this, then I also know that …’. Write these down. You are now inventing your own mathematical statements!
- Discuss your work and your thinking with your partner, and try to convince them that you are right!
Activity 2: Proving that the sum of the angles of a triangle equals 180°
Tell your students that using the facts about angles of a line intersecting parallel lines can prove that the sum of the angles of a triangle equals 180°.
(It might help to read Case Study 1 to your students for this activity.)
Now tell your students:
- Have a go at putting such a proof together. Use the phrase ‘When I know this then I also know that …’ to help you in your reasoning.
- Discuss your work and your thinking with a partner, and try to convince them that you are right!
Case Study 2: Mrs Agarwal reflects on using Activities 1 and 2
This is the account of a teacher who tried Activities 1 and 2 with her secondary students.
Because they had some examples to work from, students were happy to draw what the statements could mean. They did find Euclid’s common notions somewhat difficult to understand and it led to an interesting discussion that the mathematical language they are exposed to is not that unclear in comparison!
Ranu asked whether something like ‘ A = 30° and A= B so B = 30°’ was allowed for the statement ‘Things that are equal to the same thing are also equal to one another.’ I did not confirm or deny this, because I wanted Ranu to decide whether it was a good idea. I replied by reiterating what it said in the task:
- ‘When you know this, then you also know what?’
- ‘Try and convince your partner that you are right.’
For Activity 2 I used the approach suggested. First I read the case study about Mrs Kapur’s class aloud to them; then I asked the questions from the reflection point: ‘What do you think, class – are you convinced these ideas are mathematical proofs? Will the prime minister be convinced? Should he be convinced?’ My reasons for doing so were that I thought if I asked them to prove that the sum of the angles of a triangle equals 180°, they would come up with similar proofs as the students in Mrs Kapur’s class and I wanted to start the activity with knowing this would not be considered a proof. Most students initially agreed that what Mrs Kapur’s students had come up with was a convincing proof, but a few students were not sure. I asked them why; they said they were not convinced these proofs were built on established or accepted facts. This led to a discussion about empirical evidence, what it was and why it is not allowed in mathematical proof.
Only then did I introduce Activity 2 and ask the students to play with it, try things out and experiment. This seemed to relax them and they happily worked on it, discussing their thoughts and trying out their arguments with their neighbours. Later on, we discussed their ideas with the whole class. Some proofs did not convince the rest of the class, but several students had developed solid justification for their proof.
I also found some online videos that show the proof, such as one created by the Khan Academy [see ‘Additional resources’, below]. Although I could not show it in the classroom, I did mention it to the students to make them aware of its existence.
Reflecting on your teaching practice
When you do such an exercise with your class, reflect afterwards on what went well and what went less well. Consider the questions that made the students interested and able to work, and those where you needed to clarify. Such reflection always helps with finding a ‘script’ which helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting, as Mrs Agarwal did, some quite small things that made a difference.
Pause for thought Good questions to trigger reflection are:
|
2 Is it proof?
